Question 1020882: 5) Alice is trying to send a message to Bob. Eve is an eavesdropper who randomly corrupts words sent by Alice. Because of Eve, any word sent by Alice reaches Bob correctly with a probability, p, independent of other words. Alice sends messages to Bob such that each message is 2 words long. They also exchange some code language so that if any 1 of the two words sent by Alice is received correctly by Bob, then Bob can understand the message correctly. If a message is not received correctly by Bob, he indicates that to Alice and she re-sends the message. This is continued until Bob receives the message correctly.
a)What is the probability (in terms of p) that a message sent by Alice is received incorrectly by Bob?
b)Call your solution of Problem # 5a) as q. What should be the minimum value of q if Alice wants to give Bob a 98% guarantee that she will deliver a message correctly to Bob in 2 attempts or less?
c) What should be the minimum value of p so that you can achieve the value of q you obtained in Problem # 5b)?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
5) Alice is trying to send a message to Bob. Eve is an eavesdropper who randomly corrupts words sent by Alice. Because of Eve, any word sent by Alice reaches Bob correctly with a probability, p, independent of other words. Alice sends messages to Bob such that each message is 2 words long. They also exchange some code language so that if any 1 of the two words sent by Alice is received correctly by Bob, then Bob can understand the message correctly. If a message is not received correctly by Bob, he indicates that to Alice and she re-sends the message. This is continued until Bob receives the message correctly.
a)What is the probability (in terms of p) that a message sent by Alice is received incorrectly by Bob?
b)Call your solution of Problem # 5a) as q. What should be the minimum value of q if Alice wants to give Bob a 98% guarantee that she will deliver a message correctly to Bob in 2 attempts or less?
c) What should be the minimum value of p so that you can achieve the value of q you obtained in Problem # 5b)?
Solution:
(a)
n=2
probability of correct word = p
probability of incorrect word = (1-p)
probability of incorrect (2-word) message, q = 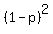
(b)
A guarantee is a guarantee (100%).
I suppose what is meant is what is the value of q such that 98% of the time, in the long run, a message will be received correctly in 2 attempts or less.
We need q^2 (both attempts fail) <=2%.
so q<=sqrt(1-98%)=0.14142 (approximately).
so maximum value of q so that the message will be received correctly in 2 attempts or less is sqrt(.02)=sqrt(2/100)=sqrt(2)/10.
(c)The minimum value of p is such that
(1-p)^2<=sqrt(2)/10
Solve for p:
1-p<=sqrt(sqrt(2)/10)
p>=1-sqrt(sqrt(2)/10)
=1-0.3761
=0.6239 (approximately)
Check:
((1-0.6239)^2)=0.02, ok.
Also,
in order that you get answers as fast as possible, I suggest you post new questions instead of in the messages. You are welcome to alert me to the question in your message if you so wish.
|
|
|