SOLUTION: To save for retirement, Karla Harby put $550 each month into an ordinary annuity for 14 years. Intrest was compounded monthly. At the end of the 14 years, the annuity was worth $15

Algebra ->  Finance -> SOLUTION: To save for retirement, Karla Harby put $550 each month into an ordinary annuity for 14 years. Intrest was compounded monthly. At the end of the 14 years, the annuity was worth $15      Log On


   

Question 1020861: To save for retirement, Karla Harby put $550 each month into an ordinary annuity for 14 years. Intrest was compounded monthly. At the end of the 14 years, the annuity was worth $157,532. What annual rate did she receive?
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
The formula for the am future value, or the amount of an ordinary annuity is
A+=+R%2A%28+%28+%281%2Br%2Fn%29%5E%28nt%29+-1%29%2F%28r%2Fn%29%29
Here, A = 157,532, R = 550, n = 12 (interest compounded monthly), t = 14 (years), and the unknown term is r, the annual interest rate.
==> 157532+=+550%2A%28+%28+%281%2Br%2F12%29%5E168+-1%29%2F%28r%2F12%29%29 after substitution, and
==>23.86848485 = 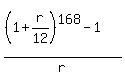%28%281%2Br%2F12%29%5E168+-1%29%2Fr (Equation A)
after further simplification.
There is no simple algebraic way of solving this equation for r, but by trial and error and using a scientific calculator, we can get quite close to the real value.
Now if r = 7%, the amount corresponding to the left-hand side of Eq'n. A is 23.669723.
If r = 7.2%, the amount corresponding to the left-hand side of Eq'n. A is 24.05381395.
the average of 7% and 7.2% is 7.1%, which gives 23.86, close to the real value of 23.86848485.
Therefore the annual interest rate rate is around 7.1%.