The other tutor gave a partial factorization but not
the complete factorization. Let's go for the complete
factorization, not just show that we can factor out 3.
 This is a third degree polynomial in three variables.
Set it equal to 0, and look for its zeros:
This is a third degree polynomial in three variables.
Set it equal to 0, and look for its zeros:


 If we assume x=-y we get
If we assume x=-y we get
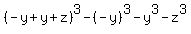







 So since x=-y gives an identity, that means that
(x+y) is a factor of the given polynomial.
In exactly the same way, by symmetry x=-z and y=-z will
also give an identity.
Therefore (x+y)(x+z)(y+z) must be a factor of the original
polynomial.
Since this will yield a third degree polynomial when
multiplied out, it can only be different from the factorization
of the original polynomial by a non-zero constant factor.
So the factorization must be:
So since x=-y gives an identity, that means that
(x+y) is a factor of the given polynomial.
In exactly the same way, by symmetry x=-z and y=-z will
also give an identity.
Therefore (x+y)(x+z)(y+z) must be a factor of the original
polynomial.
Since this will yield a third degree polynomial when
multiplied out, it can only be different from the factorization
of the original polynomial by a non-zero constant factor.
So the factorization must be:
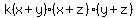 ,
for some non-zero constant k. So
,
for some non-zero constant k. So


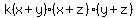 must be an identity for all values of x,y, and z
Let's choose x = 1, y = 1, z = 0
must be an identity for all values of x,y, and z
Let's choose x = 1, y = 1, z = 0
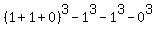

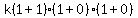
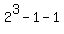

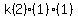
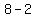

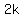


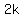


 Therefore the factorization
Therefore the factorization 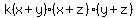 becomes
becomes
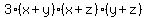 That took longer than 30 seconds! Sorry! But we got it done :)
Edwin
That took longer than 30 seconds! Sorry! But we got it done :)
Edwin