SOLUTION: Im really stuck! ABC is an isosceles triangle. The coordinates of A and B are (5,6) and (0,-4) respectively. Given that the gradient of BC is 3/4 and D is the midpoint of BC find

Algebra ->  Triangles -> SOLUTION: Im really stuck! ABC is an isosceles triangle. The coordinates of A and B are (5,6) and (0,-4) respectively. Given that the gradient of BC is 3/4 and D is the midpoint of BC find      Log On


   

Question 1020439: Im really stuck!
ABC is an isosceles triangle. The coordinates of A and B are (5,6) and (0,-4) respectively. Given that the gradient of BC is 3/4 and D is the midpoint of BC find:
Equation of AD
and
Coordinate of D,
how do i find equation of AD only with 2 points?
Found 3 solutions by Theo, Edwin McCravy, rothauserc:
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
ABC is an isosceles triangle. The coordinates of A and B are (5,6) and (0,-4) respectively. Given that the gradient of BC is 3/4 and D is the midpoint of BC find: Equation of AD and Coordinate of D.

-----

this is tough to visualize since they didn't really tell you which line was the base of the isosceles triangle and which legs were the equal legs of the triangle.

they kind of hinted at it when they asked you to find the bisector of BC, but they didn't provide you with the crucial piece of information that you need to know.

that crucial piece of information is that the bisector of the base of an isosceles triangle is the perpendicular bisector of that base.

this means the base of the isosceles triangle is BC and the congruent legs of the isosceles triangle are AB and AC.

under that assumption, you have enough information to finish your triangle.

first of all you know that your bisector must be perpendicular to BC.

second of all, you know that your perpendicular bisector will intersect with point A at (5,6).

you are given that the slope of BC is 3/4.

this means that the slope of the perpendicular bisector has to be the negative reciprocal of that.

negative reciprocal of 3/4 is equal to -(4/3).

the slope intercept form of the equation of the perpendicular bisector will be y = -(4/3)x + b.

you also know that the perpendicular bisector of BC must intersect at A.

you can solve for equation of the perpendicular bisector by one of two methods that i know.

the first is to start with y = -(4/3) + b and replace y with 6 and replace x with 5, taken from the coordinate of A, which is (5,6).

you will get 6 = -(4/3) * 5 + b

simplify to get 6 = -20/3 + b

add 20/3 to both sides of this equation to get 6 + 20/3 = b

since 6 = 18/3, this becomes 18/3 + 20/3 = b.

simplify to get 38/3 = b.

your equation of the perpendicular bisector of BC is y = -(4/3)x + 38/3.

this is the equation of the line AD.

now you want to find the coordinates for point D.

that would be at the intersection of the line BC and the line AD.

you know the equation of the line AD.

it is y = -(4/3)x + 38/3.

you need to find the equation of the line BC.

you know the slope is 3/4, so the slope intercept form of the equation is y = (3/4)x = b

you know one point of that line is (0,-4).

when you replace y with -4 and x with 0 in the equation of y = (3/4)x + b, you get -4 = 3/4 * 0 + b

solve for b and you get b = -4.

the equation of the line BC is y = (3/4)x - 4

to find the intersect, solve these two equations simultaneously.

they are:

y = -(4/3)x + 38/3
y = (3/4)x - 4

subtract the second equation from the first and you get:

0 = -(4/3)x - (3/4)x + 38/3 - (-4).

put the x terms under a common denominator and the constant terms under a common denominator and you get:

0 = -(16/12)x - (9/12)x + 38/3 + 12/3.

simplify to get:

0 = -(25/12)x + 50/3

add (25/12)x to both sides of this equation to get:

(25/12)x= 50/3

multiply both sides of this equation by 12/25 to get:

(25/12)x * (12/25) = 50/3 * 12/25

simplify to get x = 50/3 * 12/25

simplify further to get x = 8.

replace x with 8 in the original equations to get:

y = -(4/3)x + 38/3
y = (3/4)x - 4

become:

y = -(4/3)*8 + 38/3 = 2
y = (3/4)*8 - 4 = 2

the location of point D is (8,2).

you found the equation of AD by using the slope of AD and the fact that it had to intersect with point A, which was (5,6).

you also needed to find the equation of AD before you could find the location of the intersection.

your solution is:

the equation of AD is y = -(4/3)x + 38/3

point D is at (8,2).

the graph of your triangle is shown below:

$$$

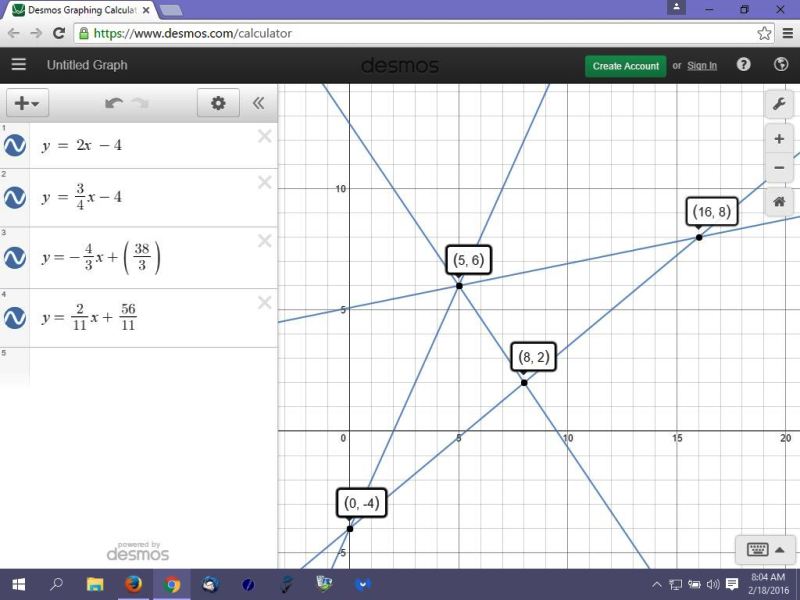
in the graph:

A is at (5,6)
B is at (0,-4)
C is at (16,8)
D is at (8,2)

you can find the equation of a straight line with only one point if you know the slope.

there are 3 basic forms for the equation of a straight line.

the slope intercept form is y = mx + b, where m is the slope and b is the y-intercept.

the standard form is ax + by = c, where a is the coefficient of the x term and b is the coefficient of the y term and c is the constat.

the point slope form is y - y1 = m * (x - x1)

if you have only one point and the slope, you can use either y = mx + b form or you can use y - y1 = m * (x - x1) form.

with the slope intercept form, you simply replace x and y with the coordinates of the known point and solve for b.

with the point slope form, you simply replace x1 and y1 with the coordinates of the known point and solve for y.

here's a reference on solving using the point slope form.

http://www.purplemath.com/modules/strtlneq2.htm






Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!




Let the unknown point D be D(h,k).

We can find the equation of AD because we are given
its gradient 3/4 and its y-intercept (0,-4)



matrix%281%2C5%2Cy%2C%22%22=%22%22%2Cexpr%283%2F4%29x%2C%22%22%2B%22%22%2C%28-4%29%29

matrix%281%2C5%2Cy%2C%22%22=%22%22%2Cexpr%283%2F4%29x%2C%22%22-%22%22%2C4%29

That's the equation of AD.

Next we find the length of AB using the distance formula:


d=sqrt%28%28x%5B2%5D-x%5B1%5D%29%5E2%2B%28y%5B2%5D-y%5B1%5D%29%5E2%29

AB=sqrt%28%28%286%29-%28-4%29%5E%22%22%29%5E2%2B%28%285%29-%280%29%29%5E2%29

AB=sqrt%28%286%2B4%29%5E2%2B%285-0%29%5E2%29

AB=sqrt%28%2810%29%5E2%2B%285%29%5E2%29

AB=sqrt%28100%2B25%29

AB=sqrt%28125%29

AB=sqrt%2825%2A5%29

AB=5sqrt%285%29

Since triangle ABC is isosceles, we know that

BC=AB=5sqrt%285%29

And since D is the midpoint of BC, then AD is
one-half of BC, so

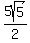BD=5sqrt%285%29%2F2

We use the distance formula and set the length 
of BD equal to this:

d=sqrt%28%28x%5B2%5D-x%5B1%5D%29%5E2%2B%28y%5B2%5D-y%5B1%5D%29%5E2%29

Square both sides of the equation:

d%5E2=%28x%5B2%5D-x%5B1%5D%29%5E2%2B%28y%5B2%5D-y%5B1%5D%29%5E2

So we have this equation, setting 5sqrt%285%29%2F2 
equal to the distance from B(0,-4) to D(h,k):



%2825%2A5%29%2F4=%28h%29%5E2%2B%28k%2B4%29%5E2

125%2F4=h%5E2%2B%28k%2B4%29%5E2

Multiply through by 4 to clear the fraction:

125=4h%5E2%2B4%28k%2B4%29%5E2

Since we know that D(h,k) is a point on line AD,
whose equation is 

matrix%281%2C5%2Cy%2C%22%22=%22%22%2Cexpr%283%2F4%29x%2C%22%22-%22%22%2C4%29

So D(h,k) it must satisfy that equation: 

k=expr%283%2F4%29h-4.

So we substitute that for k in

125=4h%5E2%2B4%28k%2B4%29%5E2

125=4h%5E2%2B4%28expr%283%2F4%29h-4%2B4%29%5E2

125=4h%5E2%2B4%28expr%283%2F4%29h%29%5E2

125=4h%5E2%2B4%2Aexpr%289%2F16%29h%5E2

125=4h%5E2%2Bexpr%289%2F4%29h%5E2

Multiply through by 4

500=16h%5E2%2B9h%5E2%29

500=25h%5E2

20=h%5E2

sqrt%2820%29=h

sqrt%284%2A5%29=h

2sqrt%285%29=h

k=expr%283%2F4%29h-4

k=expr%283%2F4%29%282sqrt%285%29%29-4

k=expr%283%2F4%29%282sqrt%285%29%29-4

k=expr%283%2F2%29sqrt%285%29-4

k=%283sqrt%285%29-8%29%2F2

So the coordinates of point D is

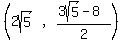%28matrix%281%2C3%2C2sqrt%285%29%2C%22%2C%22%2C%283sqrt%285%29-8%29%2F2%29%29

Edwin

Answer by rothauserc(4718) About Me  (Show Source):
You can put this solution on YOUR website!
Given D is the midpoint of B and C, then points on AD are equidistant from points B and C. AD is the perpendicular bisector.
:
Given gradient of BC is 3/4, the slope of line BC is 3/4, then
:
y = 3x/4 + b
:
: use point B, (0,-4) to find b
:
-4 = 3(0)/4 + b
:
b = -4
:
The equation of line BC is
:
y = 3x/4 -4
:
since AD is perpendicular to BC, the slope of AD is -4x/3
:
use point A, (5,6) to find b
:
6 = -4(5)/3 + b
:
18 = -20 + 3b
:
3b = 38
:
b = 38/3
:
**************************
Equation of AD is
:
y = -4x/3 + 38/3
**************************
:
Now set the two lines = to each other to find point D
:
3x/4 -4 = -4x/3 + 38/3
:
9x -48 = -16x + 152
:
25x = 200
:
x = 8
:
substitute for x in equation for BC
:
y = 3(8)/4 -4
:
y = 2
:
************************
point D is (8,2)
***********************