|
Question 1019976: please help solve this question.
Consider the function
f(x)=(x^2-1)/(x-3)
a. Find the domain for the function in interval notations
b. Find all vertical, horizontal and slant asymptotes
c. Sketch the function
d. Solve the inequality
(x^2-1)/(x-3)<1
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The domain of a function is the set of values of the independent variable for which the function is defined. For a rational function such as your example, that means the set of all real numbers except for those values that cause the denominator to equal zero.
The equation of a vertical asymptote is of the form  where where  is a value that causes the denominator function to equal zero, but does NOT cause the numerator function to be zero. If both numerator and denominator go to zero at a value, then the rational function has a discontinuity or "hole" at that point, but there is no asymptote. is a value that causes the denominator function to equal zero, but does NOT cause the numerator function to be zero. If both numerator and denominator go to zero at a value, then the rational function has a discontinuity or "hole" at that point, but there is no asymptote.
If the degree of the numerator polynomial in a rational function is LESS than the degree of the denominator function, the  -axis is the horizontal asymptote. If the degree of the numerator polynomial is EQUAL to the degree of the denominator polynomial, then the equation of the horizontal asymptote is -axis is the horizontal asymptote. If the degree of the numerator polynomial is EQUAL to the degree of the denominator polynomial, then the equation of the horizontal asymptote is  where where  is the lead coefficient of the numerator polynomial and is the lead coefficient of the numerator polynomial and  is the lead coefficient of the denominator polynomial. If the degree of the numerator polynomial is GREATER than the degree of the denominator polynomial then there is a slant (aka oblique) asymptote with an equation is the lead coefficient of the denominator polynomial. If the degree of the numerator polynomial is GREATER than the degree of the denominator polynomial then there is a slant (aka oblique) asymptote with an equation ) where where ) is the quotient excluding the remainder when the denominator polynomial is divided into the numerator polynomial using polynomial long division. is the quotient excluding the remainder when the denominator polynomial is divided into the numerator polynomial using polynomial long division.
a. Set the denominator equal to zero and solve. The domain is the set of real numbers excluding this(these) value(s).
b. Evaluate the numerator for the value(s) excluded from the domain in part a. If the numerator is NOT zero for a tested value, then there is a vertical asymptote at  equal to that value. Since your numerator has a degree larger than the degree of your denominator, there is no horizontal asymptote. Use polynomial long division to determine the equation of the slant asymptote. If you need a refresher, click Purple Math Polynomial Long Division. Be sure to read all of the relevant pages. equal to that value. Since your numerator has a degree larger than the degree of your denominator, there is no horizontal asymptote. Use polynomial long division to determine the equation of the slant asymptote. If you need a refresher, click Purple Math Polynomial Long Division. Be sure to read all of the relevant pages.
c.

d. By inspection of the graph.
John

My calculator said it, I believe it, that settles it

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
a. Since the expression for 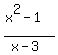 is defined for all real values of is defined for all real values of  such that such that  , ,
the domain for the function in interval notation is
  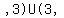   . .
b. Find all vertical, horizontal and slant asymptotes
 is a vertical asymptote, is a vertical asymptote,
because the function does not exist for  , ,
but  . .
 , ,
so  is the slant asymptote, because is the slant asymptote, because
 . .
That means the graph function "hugs" the slanted line representing  towards the left and right ends of the graph, and off course, there is no horizontal asymptote. towards the left and right ends of the graph, and off course, there is no horizontal asymptote.
We even know that  for for  , meaning the curve is above the asymptote, , meaning the curve is above the asymptote,
and  for for 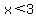 , meaning the curve is below the asymptote. , meaning the curve is below the asymptote.
c. Sketch the function
We know the asymptotes.
To sketch it, we may want to know
1)where the function is negative, zero, and positive, and
2) maxima and minima.
Since  , ,
 and and  zero. zero.
For  , , 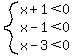 ---> --->  . .
For 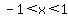 , , 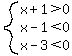 ---> ---> 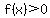 . .
For 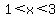 , , 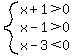 ---> --->  . .
For  , , 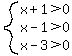 ---> ---> 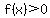 . .
To find maxima and minima, we need to calculate the derivative:
 , so , so  . .
 ---> ---> ---> ---> . .
Approximate values are  and and  . .
So  and and
 . .
We can graph the asymptotes, extreme value points, and zeros:
 , and with all else we found about , and with all else we found about  we sketch like this: we sketch like this: 
d. Solve the inequality
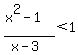
We could look at the graph and see that the solution is 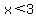 . .
Without the graph,
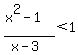 <--> <--> <--> <-->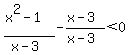 <--> <-->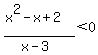
Since the denominator is always positive, the solution is 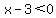 <--> <-->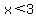 . .
|
|
|
| |