Question 1019974: I need help on solving this trig equation:
(sin2x)(cosx)+(cos2x)(sinx)=(-1/2)
Found 2 solutions by ikleyn, KMST:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need help on solving this trig equation:
(sin2x)(cosx)+(cos2x)(sinx)=(-1/2)
----------------------------------------
Apply the addition formula for sine:
sin(alpha+beta) = sin(alpha)*cos(beta) + cos(alpha)*sin(beta).
(This is one of the basis formulas in Trigonometry. See the lesson
Addition and subtraction formulas in this site).
Take  = 2x, = 2x,  = x.
Then you get your equation in this form
sin(3x) = = x.
Then you get your equation in this form
sin(3x) =  .
The solutions are
3x = .
The solutions are
3x =  + +  , k = 0, +/-1, +/-2, . . . and 3x = , k = 0, +/-1, +/-2, . . . and 3x =  + +  , k = 0, +/-1, +/-2, . . .
In terms of x the solutions are
x = , k = 0, +/-1, +/-2, . . .
In terms of x the solutions are
x = 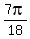 + + 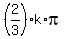 , k = 0, +/-1, +/-2, . . . and x = , k = 0, +/-1, +/-2, . . . and x =  + + 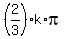 , k = 0, +/-1, +/-2, . . . , k = 0, +/-1, +/-2, . . .
Answer by KMST(5328)   (Show Source): (Show Source):
|
|
|