Question 1019853: A function f is defined for all real numbers and has the following properties.
• f(1) = 2
• f(3) = 10
• f'(2)=4
• For all real numbers a and h, f(a+h)−f(a)=kah+nh^2−2nh (where k and n are
constants).
a) Find the value of k for this function.
b) Find the value of n for this function.
c) Find a formula for f'(x) (this should just be in terms of x, it should not depend on n or k).
d) Using your answer to part c, find a formula for f(x) (this should just be in terms of x, it should not depend on n or k). Hint: Find a function g(x) such that g'(x) = f'(x).Then there is a theorem that there exists a (unique) real number c such that f(x) = g(x) + c.
How do I isolate k and n so that I'm able to find out what they equal? I'm 100% stuck on this problem, and I'm not even sure where to start at any help would be appreciated, thank you for your time.
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! We start with the difference f(3) - f(2) = k*2*1 +n -2n = 2k - n = 6, where we let a = 2 and h = 1.
==> 2k - n = 6 (Equation A)
Similarly, f(2) - f(1) = k*1*1 +n -2n = k - n = 2, where we let a = 1 and h = 1.
==> k-n = 2 (Equation B)
Solving for k and n from Equations A and B yields k = 4 and n = 2.
With these values in mind, we get
 , where we replaced a by x.
==>  , after dividing both sides by h.
==> f'(x) = 
Now f'(x) = 4x - 4 ==>  for some constant c.
We can use any one of the initial values given above to find the value of c. In particular, f(1) = 2, and so
 , which gives c = 4.
Therefore, f(x) =  .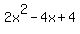
Problem solved.
|
|
|
