|
Question 1019704: Two grain-collecting machines can collect all the grain from a field 9 days faster than if the first one was doing it alone and 4 days faster than if the second one was working alone. How long does it take each grain-collecting machine to collect all the grain by itself?
Answer by ikleyn(52890)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two grain-collecting machines can collect all the grain from a field 9 days faster than if the first one was doing it alone,
and 4 days faster than if the second one was working alone. How long does it take each grain-collecting machine
to collect all the grain by itself?
--------------------------------------------------
Let f be the number of days for the first grain-collecting machines to collect all the grain from a field, if it works alone.
Let s be the number of days for the second grain-collecting machines to collect all the grain from a field, if it works alone.
Then the rate of the first machine is 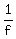 of the "field-per-day",
while the rate of the second machine is of the "field-per-day",
while the rate of the second machine is 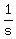 of the "field-per-day".
When both machines work simultaneously, their combined rate is of the "field-per-day".
When both machines work simultaneously, their combined rate is 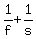 of the "field-per-day".
Hence, two machines working together can can collect all the grain from the field in of the "field-per-day".
Hence, two machines working together can can collect all the grain from the field in 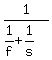 days.
Therefore, from the first part of the condition you have this equation:
f - days.
Therefore, from the first part of the condition you have this equation:
f - 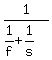 = 9. (1)
From the second part of the condition you have this equation:
s - = 9. (1)
From the second part of the condition you have this equation:
s - 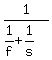 = 4. (2)
Thus you have the system of two non-linear equations (1) and (2).
Do not be scared: still there is a way to solve it.
Distract equation (2) (both sides) from equation (1). You will get
f - s = 5, or f = s + 5. (3)
Now substitute the expression f = s + 5 from (3) into equation (1). You will get a single equation for the unknown s:
(s+5) - = 4. (2)
Thus you have the system of two non-linear equations (1) and (2).
Do not be scared: still there is a way to solve it.
Distract equation (2) (both sides) from equation (1). You will get
f - s = 5, or f = s + 5. (3)
Now substitute the expression f = s + 5 from (3) into equation (1). You will get a single equation for the unknown s:
(s+5) - 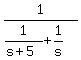 = 9.
Simplify and solve it, step by step:
(s+5) - = 9.
Simplify and solve it, step by step:
(s+5) - 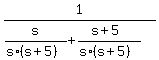 = 9, ---> s+5 - = 9, ---> s+5 - 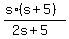 = 9, ---> . . . ---> = 9, ---> . . . --->  = =  .
To solve the last quadratic equation, factor it: .
To solve the last quadratic equation, factor it:  = (s-10)*(s+2),
and you will get the unique solution to the problem s = 10. (The other root is negative and, therefore, doesn't suit).
Answer. It will take 10 days for the second machine to complete the job working alone.
It will take 15 = 10+5 days for the first machine to complete the job working alone. = (s-10)*(s+2),
and you will get the unique solution to the problem s = 10. (The other root is negative and, therefore, doesn't suit).
Answer. It will take 10 days for the second machine to complete the job working alone.
It will take 15 = 10+5 days for the first machine to complete the job working alone.
|
|
|
| |