Question 1019409: If I have a right triangle with known side lengths, how do I find the other two angles?
The side lengths are 27,18, and 32. the only known angle is 90.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! in a right triangle, the hypotenuse is always the largest side.
the formula for the sides of a right triangle are:
one leg squared plus the other leg squared is equal to the hypotenuse squared.
in your problem, this becomes 27^2 + 18^2 = 32^2.
do the math and you get 1053 = 1024.
not eactly right on, but close enough for the problem you are being asked to solve, although it would have been better if it was right on.
if you take the square root of 1053, you get 32.44996148 which would round down to 32 if you rounded to the nearest integer.
if you solve for one of the angles, then you can find the other angle by taking its complement.
we'll solve for one of the the angles by finding the tangent of it and then solving for the angle.
the tangent of the angle is equal to one of the legs divided by the other leg.
the angle will be opposite the numerator in the equation.
so let tangent of the angle equal 18/27.
use your calculator to find the angle whose tangent is (18/27).
that angle will be 33.69006753 degrees.
the other angle will be the complement of this angle.
it will be equal to 90 - 33.69006753 = 56.30993247.
you could also have used the sine or cosine function.
in that case, you may not get the exact same answser since this is not a perfect right triangle because one leg square plus the other leg squared is not equal to the hypotenuse squared.
let's do it to see.
sine of one angle is equal to 18/32, therefore the angle is equal to the arcsine of 18/32 which is equal to 34.22886633 degrees.
sine of the the other angle is equal to 27/32, therefore the angel si equal to the arcsine of 27/32 which is equal to 57.53825503.
these angles are not the same as you got before because the right triangle is not a perfect right triangle.
for example:
consider this triangle.
one leg is 3, the other leg is 4, the hypotenuse is 5.
this triangle is a perfect right triangle because 3^2 + 4^2 = 5^2 becomes 9 + 16 = 25 which becomes 25 = 25.
using arctangent function, arctan(3/4) = 36.86989765 degrees.
using arcsin function (arcsin(3/5) = 36.86989765.
the angle is the same whether you use arctan or arcsin function.
this is because the right triangle is a perfect right triangle, unlike what you were given.
my opinion is this is a bad problem because you were not given a perfect right triangle to work with.
that's unfortunate.
hopefully you understand why.
if you solve it using arctan, and it's not the answer they're looking for, then do it using arcsin or arccos. if that don't do it, then you have other problems i'm not aware of.
if tan(x) = y, then arctan(y) = x.
if sin(x) = y, then arcsin(y) = x.
if cos(x) = y, then arccos(y) = x.
check the references after the picture shown below:
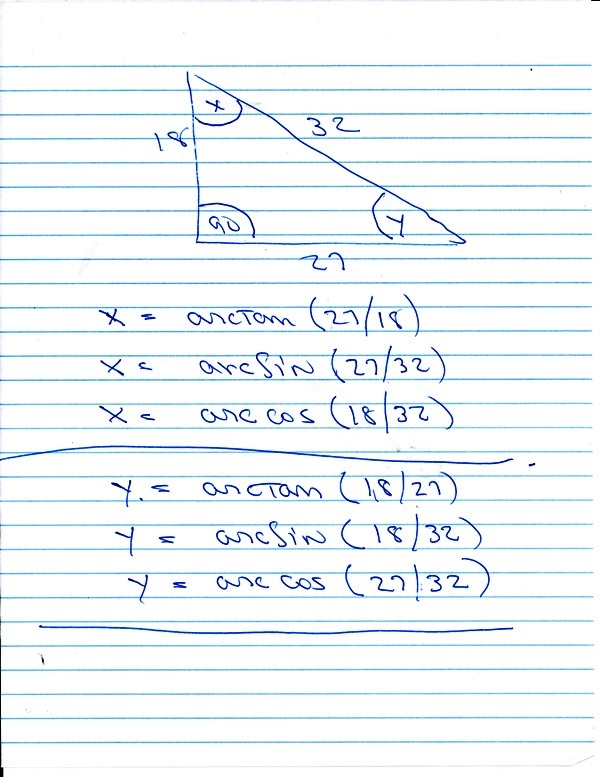
http://www.regentsprep.org/regents/math/algtrig/att1/trigsix.htm
http://www.regentsprep.org/regents/math/algebra/at1/Pythag.htm
|
|
|