|
Question 1019335: http://prntscr.com/a23h3z
So, I'm aware I have to use the distance formula.
For (-b,c) and (a,0) I got [sqroot (a+b)^2+(D-c)^2)] after simplifying it, but I don't know how to simplify any further. The same thing foes for [sqroot (-a-b)+(0-c)]. I don't know how to simplify these with the distance formula like I do if they were numbers because they're coordinates. A little help and explanation would be nice.
Answer by ikleyn(52863)   (Show Source):
You can put this solution on YOUR website! .
http://prntscr.com/a23h3z
So, I'm aware I have to use the distance formula.
For (-b,c) and (a,0) I got [sqroot (a+b)^2+(D-c)^2)] after simplifying it, but I don't know how to simplify any further. The same thing foes for [sqroot (-a-b)+(0-c)]. I don't know how to simplify these with the distance formula like I do if they were numbers because they're coordinates. A little help and explanation would be nice.
-------------------------------------------------------
The answer is  .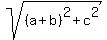
For the solution, first draw the diagonal from (-a,0) to (b,c).
Then draw the perpendicular from the point (b,c) to the base of the trapezoid.
You will get a right-angled triangle with the horizontal leg length (a + b) and the vertical leg length c.
The diagonal of the trapezoid is the hypotenuse of this triangle,
and its length is .
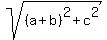Same is the length of the other diagonal.
|
|
|
| |
