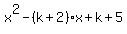
The solution using the quadratic formula:
simplifies to
We only need to require that the larger
solution, the one with the plus sign before
the square root, be negative, so
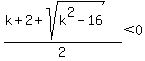The discriminant must be positive to prevent
getting 1 single or 2 imaginary solutions, so
setting the discriminant greater than 0,
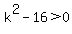That has solutions k < -4 or k > 4.
If k > 4 then certainly the larger solution
will be positive.
So we must take k < -4
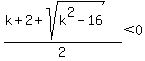Multiplying both sides by 2
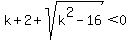
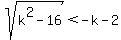
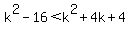
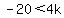
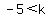Therefore to have both solutions negative,
Edwin
