SOLUTION: Suppose that a and d are integers. m and n are natural numbers such that d divides {{{a^m-1}}} and d divides {{{a^n-1}}}. Prove that d divides {{{a^gcd(m,n) -1}}}

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: Suppose that a and d are integers. m and n are natural numbers such that d divides {{{a^m-1}}} and d divides {{{a^n-1}}}. Prove that d divides {{{a^gcd(m,n) -1}}}      Log On


   

Question 1019200: Suppose that a and d are integers. m and n are natural numbers such that
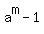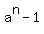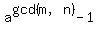
d divides a%5Em-1 and d divides a%5En-1. Prove that d divides a%5Egcd%28m%2Cn%29+-1
Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
From Bezout's lemma (or Euclidean algorithm), there exist integers and such that .

Since is divisible by d, then . Note that the exponent could be negative, but this is okay, since this still obeys the rules of modular arithmetic (if e > 0, then , where is defined as the integer such that (if an inverse exists). In particular, a and d are relatively prime, so an inverse of a exists mod d.

Similarly, .

It follows that , or is divisible by d. Since we expressed gcd(m,n) = xm + yn, it follows that d divides .