Question 1018511: if a1,a2,a3.... are in A.P Such tgat a2/a7=3/2, then the 13th term of A.P is
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a1,a2,a3.... are in A.P such that a2/a7=3/2, then the 13th term of A.P is
------------------------------------------------------------------------
Please check your condition.
I was able to conclude that the 17th term is zero.
But there is no info to guess the 13th term.
OK, we have a disputed issue.
Let me put my arguments.
1.
We have  = = 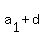 , ,  = = 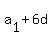 ,
where ,
where  is the first term of the AP and d is the common difference.
We also have an equation is the first term of the AP and d is the common difference.
We also have an equation
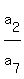 = =  , (1)
which is the same as , (1)
which is the same as
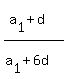 = =  . (2)
From (2) we have . (2)
From (2) we have
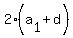 = = 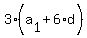 , or , or
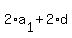 = = 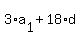 , or , or
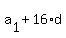 = =  . (3)
The left side, . (3)
The left side, 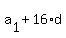 , is nothing else as , is nothing else as  .
Therefore, (3) means that .
Therefore, (3) means that  = =  ,
exactly as I said at the very beginning of my post.
2.
Now, my second statement is: from the given condition we can not make any conclusion about the concrete value of any term of this AP,
unless it is zero.
Indeed, we can multiply all terms of the given AP by an arbitrary non-zero number. The condition (1) still will be held, but the
concrete value of ,
exactly as I said at the very beginning of my post.
2.
Now, my second statement is: from the given condition we can not make any conclusion about the concrete value of any term of this AP,
unless it is zero.
Indeed, we can multiply all terms of the given AP by an arbitrary non-zero number. The condition (1) still will be held, but the
concrete value of  , let say, will be multiplied by this arbitrary factor.
Only if the term of the AP is zero, it will not be changed after multiplication.
So, based on given conditions, we can make quantitative suggestion only about the zero term of the AP. , let say, will be multiplied by this arbitrary factor.
Only if the term of the AP is zero, it will not be changed after multiplication.
So, based on given conditions, we can make quantitative suggestion only about the zero term of the AP.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|