Question 1018478: How would I solve (3x+2/x+1) > 4 ? Thank you for your help
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
How would I solve (3x+2/x+1) > 4 ? Thank you for your help
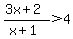 , with , with 
3x + 2 > 4(x + 1) ------- Multiplying by LCD, x + 1
3x + 2 > 4x + 4
3x - 4x > 4 - 2
- x > 2
 ------> ------> 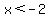
We now have 2 critical points: - 2 and - 1, and 3 INTERVALS to check:
1) x < - 2, or x = - 3 (- 3 was chosen since - 3 < - 2)
2) - 2 < x < - 1, or x = - 1.5 (this is a value between - 2 and - 1)
3) x > - 1, or x = 0 (0 was chosen since 0 > - 1)
1) x < - 2, or x = - 3
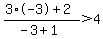 ----- Substituting - 3 in original inequality ----- Substituting - 3 in original inequality
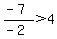
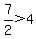 ------- False, so x < - 2 is NOT a solution, as this interval DOES NOT satisfy the inequality ------- False, so x < - 2 is NOT a solution, as this interval DOES NOT satisfy the inequality
2) - 2 < x < - 1, or x = - 1.5
 ----- Substituting - 1.5 in original inequality ----- Substituting - 1.5 in original inequality
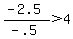
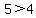 ------- TRUE, so ------- TRUE, so  IS a solution, as this interval DOES satisfy the inequality IS a solution, as this interval DOES satisfy the inequality
3) x > - 1, or x = 0
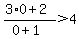 ----- Substituting 0 in original inequality ----- Substituting 0 in original inequality

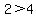 ------- False, so x > - 1 is NOT a solution, as this interval DOES NOT satisfy the inequality ------- False, so x > - 1 is NOT a solution, as this interval DOES NOT satisfy the inequality
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How would I solve (3x+2/x+1) > 4 ? Thank you for your help
-----------------------------------------------------------
 > >  . (1) . (1)
Now see how it SHOULD be done.
1. First, let us assume that x+1 > 0.
In other words, we will consider now real numbers { x | x > -1 }.
Multiply both side of (1) by (x+1), which is positive in this case. Then you will get
3x+2 > 4*(x+1) ---> 3x+2 > 4x+4 ---> 2-4 > 4x-3x ---> -2 > x.
Thus we obtain this: if x > -1, then x < -2.
It is, surely, absurd.
So, in the domain x > -1 there is no solution to (1).
2. Next, let us consider the interval x < -1. In this interval, the denominator (x+1) is negative.
Multiply both side of (1) by (x+1), which is negative now. Then you will get
3x+2 < 4*(x+1). (2)
Notice, that I changed the sign ">" of the inequality to the opposite sign "<", when I multiplied both sides of (1) by negative number (x+1).
Further, (2) implies 3x+2 < 4x+4 ---> 2-4 < 4x-3x ---> -2 < x, or x > -2.
Thus we obtain this: if x < -1, then x > -2.
It means that the set of real numbers -2 < x < -1 satisfies the inequality (1).
It is the solution of the inequality (1).
Answer. The solution to (1) is the interval (-2,-1).
Below is the plot, for illustration.

Figure 1. Plot y = 
|
For similar problems, see the lesson Solving inequalities for rational functions with non-zero right side in this site.
|
|
|