SOLUTION: A quadrilateral contains an inscribed circle. The ratio of the perimeter of the quadrilateral to that of the circle is 4:3. Find the ratio of the area of the quadrilateral to that

If a quadrilateral has/contains an inscribed circle, then the area of the quadrilateral is 


 = ,


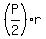where P is the quadrilateral's perimeter, and r is the radius of the inscribed circle.

It is well known fact. See the lesson Area of a quadrilateral circumscribed about a circle in this site. 

From the other side, the circumference of the circle is  = , and the area of the circle S is  = .

Therefore,

 =  :  = .

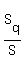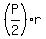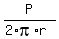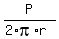Now recall that   = ,  it is given.

Hence,   = .

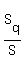The solution is complete.