SOLUTION: A triangle with sides 17cm, 39cm and 44cm contains an inscribed circle with circumference 13 1/5 pi cm. what is the area of part of the triangle that is outside the inscribed circl

Algebra ->  Pythagorean-theorem -> SOLUTION: A triangle with sides 17cm, 39cm and 44cm contains an inscribed circle with circumference 13 1/5 pi cm. what is the area of part of the triangle that is outside the inscribed circl      Log On


   

Question 1018155: A triangle with sides 17cm, 39cm and 44cm contains an inscribed circle with circumference 13 1/5 pi cm. what is the area of part of the triangle that is outside the inscribed circle? Express your answer in terms of pi.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
For a circle of radius R ,
circumference=2%2Api%2AR and
area=pi%2AR%5E2 ,
so for the circle in this problem
2%2Api%2AR=13%261%2F5cm=%2866%2F5%29%2Apicm-->R=33%2F5cm=6.6cm , and
area=pi%2A6.6cm%5E2=43.56picm%5E2 .

For a triangle with side length a , b , and c ,
the area can be calculated using Heron's formula as
area=sqrt%28s%28s-a%29%28s-b%29%28s-c%29%29 where s is the semiperimeter (half the perimeter),
calculated as s=%28a%2Bb%2Bc%29%2F2 .
For the triangle in the problem,
s=17cm%2B39cm%2B44cm%29%2F2=100cm%2F2=50cm ,
and the area, in cm%5E2 , is
area=sqrt%2850%2A%2850-17%29%2A%2850-39%29%2A%2850-44%29%29=sqrt%2850%2A33%2A11%2A6%29=330 .
So, with the area of the triangle being 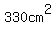330cm%5E2
and the area of the circle being 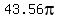43.56picm%5E2 ,
the area of the part of the triangle that is outside the inscribed circle is
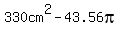330cm%5E2-43.56picm%5E2=highlight%28matrix%281%2C2%2C%28330-43.56pi%29%2Ccm%5E2%29%29 .

IF YOU REALLY HAVE TO USE THE PYTHAGOREAN THEOREM,
you can solve the triangle as solver did for the same question posted as question number 1018159:

green%28h%29=sqrt%2817%5E2-x%5E2%29=sqrt%2839%5E2-%2844-x%29%5E2%29
sqrt%2817%5E2-x%5E2%29=sqrt%2839%5E2-%2844-x%29%5E2%29
17%5E2-x%5E2=39%5E2-%2844%5E2%2Bx%5E2-88x%29
17%5E2-x%5E2=39%5E2-44%5E2-x%5E2%2B88x%29
17%5E2=39%5E2-44%5E2%2B88x%29
17%5E2-39%5E2%2B44%5E2=88x%29
289-1521%2B1936=88x%29
704=88x%29--->x=704%2F88=8
So, green%28h%29=sqrt%2817%5E2-8%5E2%29=sqrt%28289-64%29=sqrt%28225%29=15 ,
and the area of the triangle, in cm%5E2 is
area=44%2A15%2F2=330 .

Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.
A triangle with sides 17cm, 39cm and 44cm contains an inscribed circle with circumference 13 1/5 pi cm. what is the area of part of the triangle that is outside the inscribed circle? Express your answer in terms of pi.
----------------------------------------------------------------- 

The triangle with sides 17, 39 and 44 is Heronian triangle 

It has the perimeter of 100 units (halpf of the perimeter is 50 units), and the area of 330 square units. 

(To find the area, apply the Heronian formula. See the lesson Proof of the Heron's formula for the area of a triangle in this site).

The radius of the inscribed circle is 330%2F50 = 33%2F5 = 63%2F5 units.

(See the lesson Proof of the formula for the area of a triangle via the radius of the inscribed circle in this site).

So, the circumference of the inscribed circle is 2%2Api%2Ar = 131%2F5 units.

Therefore, there is no need to include this data into the condition. It is calculated from the triangle side measures by the unique way.

The answer to your question is   330 - pi%2A%2833%2F5%29%5E2.