.
find the three numbers in an arithmetic progression whose sum is 48 and the sum of their squares is 800
----------------------------------------------------
One can present the three consecutive terms of the AP as
x -d, x, x + d,
where x is the mid term and d is the common difference.
Then the sum of the tree terms is 3x, and you can easily find a from the equation
3x = 48,
which implies x =  = 16.
Now the sum of squares of the tree terms is
= 16.
Now the sum of squares of the tree terms is
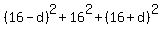 =
= 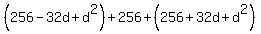 =
= 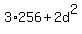 =
= 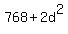 .
It gives you an equation to find d:
.
It gives you an equation to find d:
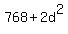 =
= 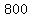 --->
--->  =
= 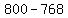 = 32 --->
= 32 --->  =
= 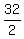 = 16.
Hence, d = +/- 4.
It gives the AP terms as 12, 16 20, or 20, 16, 12.
Answer. AP terms are 12, 16 20, or 20, 16, 12.
= 16.
Hence, d = +/- 4.
It gives the AP terms as 12, 16 20, or 20, 16, 12.
Answer. AP terms are 12, 16 20, or 20, 16, 12.