Question 1017163: I am 43 and haven't mess with this kind of math since the 90's. I am starting to understand of it, but still have trouble with word problems and setting them up.
A logistics company uses two different models of computers in their office. The first model costs $45 to upgrade and the second model costs $30 to upgrade. If the company upgrades 200 computers and it costs $7,125 in total, how many units of each model are upgraded?
Found 2 solutions by ikleyn, fractalier:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
I am 43 and haven't mess with this kind of math since the 90's. I am starting to understand of it, but still have trouble with word problems and setting them up.
A logistics company uses two different models of computers in their office. The first model costs $45 to upgrade and the second model costs $30 to upgrade. If the company upgrades 200 computers and it costs $7,125 in total, how many units of each model are upgraded?
-----------------------------------------------------
Let x = the number of computers that costs $30 to upgrade.
Then the number of others computers is 200 - x.
Now let us write the balance:
30*x + 45*(200-x) = 7125.
We need solve this equation for x. For it, simplify the equation:
30x + 45*200 - 45x = 7125.
-15x = 7125 - 45*200 = 7125 - 9000 = -1875.
Hence, x = 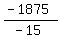 =  = 125.
Thus there are 125 computers to upgrade for $30.
And 200 - 125 = 75 computers to upgrade for $45.
Answer by fractalier(6550)  (Show Source):
You can put this solution on YOUR website! Let us call the numbers of each of the upgraded models, x and y.
Then we can write as our number equation
x + y = 200 and the cost equation would be
45x + 30y = 7125
Now what we will do is multiply the first equation by 45 and subtract it from the second equation...we get
45x + 30y = 7125
-(45x + 45y = 9000)
-------------------
-15y = -1875
Now divide by -15 and get
y = 125 units @ $30 and then
x = 200 - y = 75 units @ $45
(Good to see you back in school!)
|
|
|
