Question 1016873: a+(1/(b+1/c)=37/16
find a,b and c if a,b and c are positive integers
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! 
Upon reduction, the left-hand side becomes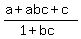 
We can let 1 + bc = 16, or bc = 15. (Assuming the top and bottom are relatively prime.)
==>a + abc + c = a + 15a +c = 16a + c = 37.
Since b and c are positive integers, the only possibilities for b and c are as follows:
b = 1, c = 15
b = 3, c = 5
b = 5, c = 3
b = 15, c = 1
From 16a + c = 37, only the value c = 5 will give a positive integer value of a = 2. Therefore, a = 2, b = 3, and c = 5.
|
|
|
