|
Question 1016826: show that the points(1,-3),(3,2),(-2,4) are the vertices of an isosceles triangle and find its area.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! Pick any two points to serve as a base for finding the area.
Points (1,-3) and (3,2):
 .
The line containing those points is...
Use that line, and the not-yet-used vertex point of (-2,4).
What is equation of the line perpendicular to the chosen base and containing point (-2,4)?
What is the "height" of the triangle, using this point (-2,4) as one endpoint?
Find the intersection point of  and  .
Skipping the steps here, that intersection point is ( 87/34, 43/34 ).
-
The height you want is  .
Simplify this as much as possible.
Your goal is to use area formula  .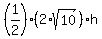
------
To show that the triangle is isosceles, just use Distance Formula between the three segments.
Answer by ikleyn(52814)  (Show Source):
You can put this solution on YOUR website! .
show that the points (1,-3), (3,2), (-2,4) are the vertices of an isosceles triangle and find its area.
---------------------------------------------------------
This is your triangle.
1. From this plot you can see (visually) that it is isosceles.
You can check it by calculating the lengths of the corresponding sides.
2. You can see (visually) also that it is right-angled triangle.
You can check it algebraically.
3. When you know two legs dimensions, you can calculate the area
of the triangle as half of the product of its legs dimensions.
|
|
|
| |
