Question 1016825: show that the points(4,0),(2,1),(-1,-5) are the vertices of a right triangle and find its area.
Answer by ikleyn(52829)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
show that the points (4,0), (2,1), (-1,-5) are the vertices of a right triangle and find its area.
----------------------------------------------------------
This is your triangle.
Calculate the distances between the given points (4,0), (2,1), (-1,-5).
1. Points (4,0) and (2,1). The distance a = 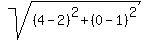 = = 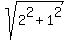 = =  .
2. Points (2,1) and (-1,-5). The distance b = .
2. Points (2,1) and (-1,-5). The distance b =  = = 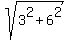 = =  = =  .
3. Points (4,0) and (-1,-5). The distance c = .
3. Points (4,0) and (-1,-5). The distance c =  = = 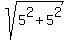 = = 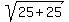 = = 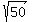 .
Now you see that .
Now you see that  + +  = 5 + 45 = 50 = = 5 + 45 = 50 =  .
It is just enough to conclude that the triangle is right-angled.
Next, the area of the triangle is .
It is just enough to conclude that the triangle is right-angled.
Next, the area of the triangle is  = = 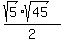 = = 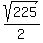 = =  = 7.5 = 7.5  . .
|
|
|