SOLUTION: Balls are printed in a pattern. Every 18th ball has stripes, every 15th ball has polka dots, and every 30th ball has stars. a) How many balls must be printed to get the first ball

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Balls are printed in a pattern. Every 18th ball has stripes, every 15th ball has polka dots, and every 30th ball has stars. a) How many balls must be printed to get the first ball      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1016707: Balls are printed in a pattern. Every 18th ball has stripes, every 15th ball has polka dots, and every 30th ball has stars.
a) How many balls must be printed to get the first ball with stripes, polka dots, and stars?
b) How many balls have been printed at that point that have only two of the designs?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
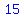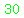a) The ordinal number of the first ball with all 3 designs is the least common multiple of red%2818%29 , blue%2815%29 , and green%2830%29 .
That number is highlight%2890%29=3%2Agreen%2830%29=6%2Ablue%2815%29=5%2Ared%2818%29 .
The highlight%2890th%29 ball has all 3 designs.
How do we find it? Let me count the ways.
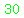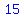1) We could start checking increasing multiples of green%2830%29 until we find one that is also a multiple of red%2818%29 , and blue%2815%29 .
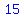1%2Agreen%2830%29=2%2Ablue%2815%29 is already a multiple of blue%2815%29 ,
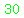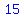so all multiples of green%2830%29 will be multiple of blue%2815%29 ,
but 1%2Agreen%2830%29 is not a multiple of red%2818%29 ,
and neither is 2%2Agreen%2830%29=60 ,
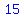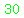but 3%2Agreen%2830%29=5%2Ared%2818%29=highlight%2890%29 is the first common multiple of red%2818%29 , blue%2815%29 , and green%2830%29 that we find.
2) We could start from the prime factorizations:
red%2818%29=2%2A9=2%2A3%5E2 ,
blue%2815%29=3%2A5 , and
green%2830%29=3%2A10=2%2A5%2A3 ,
so the least common multiple must contain the prime factors 2 , 3 , and 5 ,
and we need the 3 to be squared, as it is in red%2818%29=2%2A3%5E2 ,
so the least common multiple is 2%2A3%5E2%2A5=2%2A9%2A5=10%2A9=highlight%2890%29 .

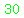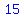b) We already saw in 1) above that all multiples of green%2830%29 are multiples of blue%2815%29 ,
so the balls number green%2830%29=2%2Ablue%2815%29 and 60=2%2Agreen%2830%29=4%2Ablue%2815%29 have two designs:
polka dots, and stars, but not stripes.
So by the time the first ball with all three designs, the 90th ball, is printed,
at least highlight%282%29 balls, the 30th and the 60th one, will have been printed with only two designs:
polka dots, and stars, but not stripes.
Are there any other balls before the 90th ball that have two designs?
Maybe stripes and polka dots, or stripes and stars?
NO, there is none.
Any multiple of red%2818%29=2%2A9=2%2A3%5E2 , and blue%2815%29=3%2A5 ,
or red%2818%29=2%2A9=2%2A3%5E2 , and green%2830%29=3%2A10=2%2A5%2A3 ,
must be a multiple of all three numbers.
It must have 2 , 3%5E2 , and 5 in its factorization,
so it will be a multiple of 2%2A3%5E2%2A5=90 .
If a ball has stripes and one another design printed, it has all three designs.