SOLUTION: I need help trying to solve this problem. Thank you in advance, for helping me out. I really appreciate your time and efforts. Have a terrific day :) Here is the question: The r

Algebra ->  Probability-and-statistics -> SOLUTION: I need help trying to solve this problem. Thank you in advance, for helping me out. I really appreciate your time and efforts. Have a terrific day :) Here is the question: The r      Log On


   

Question 1016582: I need help trying to solve this problem. Thank you in advance, for helping me out. I really appreciate your time and efforts. Have a terrific day :) Here is the question:
The range is completed determined by the two extreme scores in a distribution. The standard deviation for the following sample of n= 5 scores. Note that there are three scores clustered around the mean in the center of the distribution, and two extreme values.
Scores: 0, 6, 7, 8, 14.
B. Now we will break up the cluster in the center of the distribution by moving two of the central scores out to the extremes. Once again compute the range and the standard deviation.
New scores: 0, 0, 7, 14, 14.
C. According to the range, how do the two distributions compare in variability? How do they compare according to the standard deviation?
Yours,
John Cruz
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The range is the maximum value minus the minimum value,
so in both cases the range is 14-0=14 .
You notice that the middle value (called the median) is 7 ,
and that happens to also be the mean or average,
because %28%280%2B6%2B7%2B8%2B14%29%29%2F5=35%2F5=7 .
The set 0, 6, 7, 8, 14 has
three scores clustered around the mean in the center of the distribution (6, 7, and 8),
and two extreme values (0, and 14).
When you replace 0 for 6 and 14 for 8 ,
you get 0,0,7,14,14,
which also has 7 and the mean, %28%280%2B0%2B7%2B14%2B14%29%29%2F5=35%2F5=7 ,
and also as the median.
All the other values are as far from 7 as possible,
while still having a range of 14 .
The values in the set 0,0,7,14,14 are more spread out,
showing more variability.
The range does not show that.
It only takes into account the extreme values,
and so it is the same for the two sets: 14-0=14 .
The standard deviation does show the different variability,
because it takes into account how different from the mean all the values are.
The standard deviation can be calculated by using a calculator or some computer program.
Otherwise, you can
calculate the differences between each value and the mean,
square them,
calculate the average of those squares,
and then take the square root of the result.
For the set 0,0,7,14,14, the differences from the mean are
0-7=-7 , 0-7=-7 , 7-7=0 , 14-7=7 , and 14-7=7 .
The squares of those differences are
%28-7%29%5E2=49 , %28-7%29%5E2=49 , 0%5E2=0 , 7%5E2=49 , and 7%5E2=49 .
Their average is %28%2849%2B49%2B0%2B49%2B49%29%29%2F5=4%2A49%2F5 .
The square root of that is
,
which can be more elegantly written as 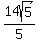14sqrt%285%29%2F5 .
For the set 0,6,7,8,14, the differences from the mean are
0-7=-7 , 6-7=-1 , 7-7=0 , 8-7=1 , and 14-7=7 .
The squares of those differences are
%28-7%29%5E2=49 , %28-1%29%5E2=1 , 0%5E2=0 , 1%5E2=1 , and 7%5E2=49 .
Their average is %28%2849%2B1%2B0%2B1%2B49%29%29%2F5=100%2F5 .
The square root of that is
sqrt%28100%2F5%29=sqrt%28100%29%2Fsqrt%285%29=10%2Fsqrt%285%29 ,
which can be more elegantly written as 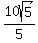10sqrt%285%29%2F5 .
Comparing the two sets' standard deviations, we find that
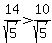14%2Fsqrt%285%29%3E10%2Fsqrt%285%29 , which showa that the set 0,0,7,14,14, has more variability.
Of course we knew that, because we made it so,
by moving the values 6 and 8 away from the mean 7 .