SOLUTION: How would I solve the following rational inequality: (x-5/3x) < 3 Thank you for your help

 < 3.   (1)


1. Assume that x > 0.
   
   Multiply both sides of (1) by 3x, which is positive in this case. You will get an inequality

  x - 5 < 9x  --->  -5 < 8x  --->  x > .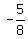

  Thus he solution in this case is the set of real {x | x > 0}, i.e the interval (,).


2. Assume that x < 0.
   
   Multiply both sides of (1) by 3x, which is negative in this case. You will get an inequality

  x -5 > 9x  --->  -5 > 8x  --->  x < 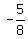.   <----  Notice that I changed the inequality sign when multiplied by negative number!

  Thus he solution in this case is the set of real {x | x < 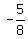 }, i.e the semi-infinite interval (,).

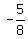Answer. The solution is the union of two intervals: (,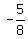) U (,).

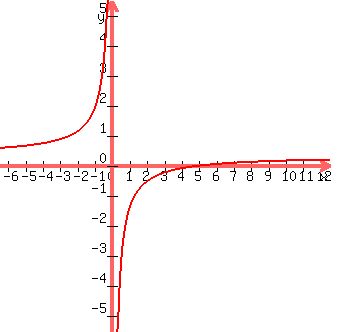
Figure. Plot y =