SOLUTION: find k if kx+y+z=4-k x+ky+z=2+k x+y+kz=3 for 1-unique solu 2-infinite solu 3-no solu

Algebra ->  Matrices-and-determiminant -> SOLUTION: find k if kx+y+z=4-k x+ky+z=2+k x+y+kz=3 for 1-unique solu 2-infinite solu 3-no solu      Log On


   

Question 1015937: find k if
kx+y+z=4-k
x+ky+z=2+k
x+y+kz=3
for
1-unique solu
2-infinite solu
3-no solu
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Look at the coefficient matrix,
A=%28matrix%283%2C3%2C%0D%0Ak%2C1%2C1%2C%0D%0A1%2Ck%2C1%2C%0D%0A1%2C1%2Ck%29%29
Find the determinant,
D=k%28k%5E2-1%29%2B1%281-k%29%2B1%281-k%29
D=k%5E3-k%2B2-2k
D=k%5E3-3k%2B2
D=%28k-1%29%5E2%28k%2B2%29
So k=1 and k=-2 are solutions.
When k=1,
A=%28matrix%283%2C3%2C%0D%0A1%2C1%2C1%2C%0D%0A1%2C1%2C1%2C%0D%0A1%2C1%2C1%29%29
and the right hand side becomes,
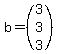
b=%28matrix%283%2C1%2C3%2C3%2C3%29%29
So this system is dependent and has infinitely many solutions.
.
.
When k=-2,
A=%28matrix%283%2C3%2C%0D%0A-2%2C1%2C1%2C%0D%0A1%2C-2%2C1%2C%0D%0A1%2C1%2C-2%29%29
and the right hand side becomes,
b=%28matrix%283%2C1%2C6%2C0%2C3%29%29.
In this case, it is an inconsistent system because 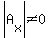abs%28A%5Bx%5D%29%3C%3E0,
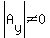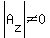abs%28A%5By%5D%29%3C%3E0, and abs%28A%5Bz%5D%29%3C%3E0,
.
.
For all other values of k, you would have a unique solution.