SOLUTION: I have tried this using our book and I just don't udestand the process. My teacher is of no help, she just keeps pointing me to our book. Factor each polynomial completely. a

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I have tried this using our book and I just don't udestand the process. My teacher is of no help, she just keeps pointing me to our book. Factor each polynomial completely. a      Log On


   

Question 101585: I have tried this using our book and I just don't udestand the process. My teacher is of no help, she just keeps pointing me to our book.
Factor each polynomial completely.
a) x^3y+2x^2y^2+xy^3
b) -4w^3-16w^2+20w
c) 3x^2 – 17x + 10
Thank you so much for any help you can provide me with. :)
d) -36a^2b + 21ab^2 – 3b^3
Answer by ptaylor(2198) About Me  (Show Source):
You can put this solution on YOUR website!
I have tried this using our book and I just don't udestand the process. My teacher is of no help, she just keeps pointing me to our book.
Factor each polynomial completely.
a) x^3y+2x^2y^2+xy^3
b) -4w^3-16w^2+20w
c) 3x^2 – 17x + 10
Thank you so much for any help you can provide me with. :)
d) -36a^2b + 21ab^2 – 3b^3

a) 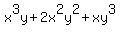x%5E3y%2B2x%5E2y%5E2%2Bxy%5E3 by inspection, we see that we can take an xy out of each term so lets do that:
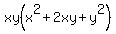xy%28x%5E2%2B2xy%2By%5E2%29 Again, by inspection, we see that x%5E2%2B2xy%2By%5E2 is a perfect square%28x%2By%29%5E2 but we can also do the following:
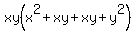xy%28x%5E2%2Bxy%2Bxy%2By%5E2%29 and we can re-write this as follows:
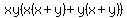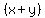xy%28x%28x%2By%29%2By%28x%2By%29%29 now we can factor out an%28x%2By%29 and we get:
xy%28x%2By%29%28x%2By%29 or
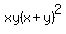xy%28x%2By%29%5E2------------------ans

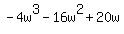b) -4w%5E3-16w%5E2%2B20w+ by inspection, we see that we can take a -4wout of each term so lets do that:
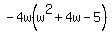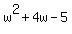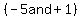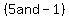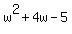-4w%28w%5E2%2B4w-5%29 Now we observe that w%5E2%2B4w-5 is a quadratic in standard form. When we have a quadratic in standard form and the A coefficient is 1 then the B coefficient is the sum of the factors of the C coefficent. What are the factors of the C coefficient?? They can only be %28-5+and+%2B1%29 or %28%2B5+and+-1%29. By inspection we see that +5 and -1=+4. 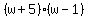So now we know that: w%5E2%2B4w-5=%28w%2B5%29%28w-1%29. Now putting it all back together, we have:
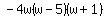-4w%28w-5%29%28w%2B1%29---------------------ans
c) 3x%5E2+%96+17x+%2B+10 Here are the possibilities:
By inspection, we see that if this quadratic can be factored, then the factors must be of the form (a-b)(c-d) or (c-b)(a-d). Why??? Because the last term is positive and the middle term is negative. So here are the possibilities:
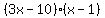
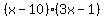
1. %283x-10%29%28x-1%29
2. %28x-10%29%283x-1%29
3. %283x-5%29%28x-2%29
4. %28x-5%29%283x-2%29
Expanding each of the above using the FOIL crutch (First, Inner, Outer, Last) we get:
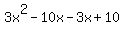1.3x%5E2-10x-3x%2B10-----------------NO!!! inner term is -13x
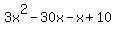2.3x%5E2-30x-x%2B10------------------NO!!! inner term is -31x
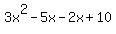3.3x%5E2-5x-2x%2B10-------------------NO!!!! inner term is -7x
4.3x%5E2-15x-2x%2B10----------------BINGO!!!!!!!
%28x-5%29%283x-2%29-----------------------ans
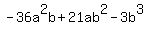d) -36a%5E2b%2B21ab%5E2-3b%5E3 By inspection, we see that we can take a -3b out of each term:
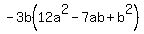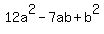-3b%2812a%5E2-7ab%2Bb%5E2%29 Now use the approach that was used in (c) above and find the factors for 12a%5E2-7ab%2Bb%5E2 . I bet you can do it!!!!!

Hope this helps---ptaylor