SOLUTION: Find all x in the interval (0, pi) that satisfy: cot(x/2)>1+cot(x)

Algebra ->  Trigonometry-basics -> SOLUTION: Find all x in the interval (0, pi) that satisfy: cot(x/2)>1+cot(x)      Log On


   

Question 1015049: Find all x in the interval (0, pi) that satisfy:
cot(x/2)>1+cot(x)
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
We know that tanx+=+%282tan%28x%2F2%29%29%2F%281-%28tan%28x%2F2%29%29%5E2%29, and so by inverting,
cotx+=+%281-%28tan%28x%2F2%29%29%5E2%29%2F%282tan%28x%2F2%29%29.
The original inequality then becomes

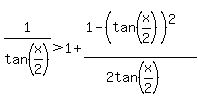1%2Ftan%28x%2F2%29+%3E1+%2B+%281-%28tan%28x%2F2%29%29%5E2%29%2F%282tan%28x%2F2%29%29, or


2%2F%282tan%28x%2F2%29%29+%3E1+%2B+%281-%28tan%28x%2F2%29%29%5E2%29%2F%282tan%28x%2F2%29%29.
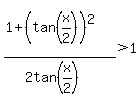
==> %281%2B%28tan%28x%2F2%29%29%5E2%29%2F%282tan%28x%2F2%29%29%3E1
The fact that x is in (0,pi) means that x/2 is in (0, pi/2), in which case tan(x/2) is always POSITIVE and so the last inequality becomes
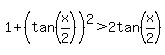1%2B%28tan%28x%2F2%29%29%5E2+%3E+2tan%28x%2F2%29.
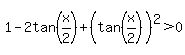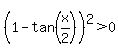==> 1-2tan%28x%2F2%29%2B%28tan%28x%2F2%29%29%5E2+%3E0+, or %281-tan%28x%2F2%29%29%5E2+%3E+0.
The last inequality is always true except when 1 - tan(x/2) = 0. This happens only when x%2F2+=+pi%2F4, or x+=+pi%2F2.
Therefore, the solution set of the inequality is (0,pi/2) U (pi/2,pi).