SOLUTION: For the equation {{{x^4 + x^3 -16x^2 -4x +48=0}}} the product of two of the roots is 6. Hence express the equation in the form {{{(x^2+ax+b)(x^2+cx+d)=0}}} Find the roots of

You are to express the 4th degree polynomial equation in this form:



Fact 1.  A polynomial equation has the same number of roots as 
its degree, including duplicate roots.

Fact 2: A monic polynomial is a polynomial with leading 
coefficient 1.

Fact 3:  The constant term of a monic polynomial is the product
of the roots if the degree is even [and the negative of the
product of the roots if the degree is odd].  

By fact 1,  has 4 roots.

by fact 3, the product of all four roots is 48.

We are told that the product of two of the roots is 6.
Since we know that the product of ALL the roots is 48, and 
the product of two of them is 6, the product of the other 
two roots must be 48/6 = 8

Let  be the quadratic whose two roots have 
product 6.  Then by the fact 3 above, b=6

Let  be the quadratic whose two roots have 
product 8.  Then by the fact 3 above, d=8.

So we have the identity:



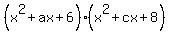Multiply out the right side:



Equate the terms in 



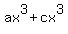Divide through by 



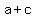Equate the terms in 



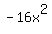Divide through by 





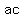Equate the terms in 



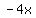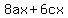Divide through by 



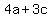So we have the three equations:



Solve any two of those by substitution or elimination
and get a=-5 and c=6.

So  in the form



is  



To find the roots of the equation, factor each of those



Set each factor = 0 and the roots are:

2, 3, -4, and -2

Edwin