SOLUTION: Show that nPr = nPr+1 (show that n permutation r equals to n permutation r+1).

Algebra ->  Permutations -> SOLUTION: Show that nPr = nPr+1 (show that n permutation r equals to n permutation r+1).      Log On


   

Question 1014498: Show that nPr = nPr+1 (show that n permutation r equals to n permutation r+1).
Answer by mathmate(429) About Me  (Show Source):
You can put this solution on YOUR website!

Question:
Show that nPr = nPr+1 (show that n permutation r equals to n permutation r+1)

Solution:
We will use the notation P%28n%2Cr%29=nPr=n%21%2F%28n-r%29%21, so that
if and when
P(n,r)=P(n,r+1), then
P(n,r)-P(n,r+1)=0.............(1)
expanding above
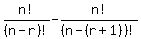n%21%2F%28n-r%29%21-n%21%2F%28n-%28r%2B1%29%29%21=0
n%21%2F%28n-r%29%21-n%21%2F%28n-r-1%29%21=0
Add by cross multiplication:
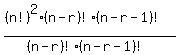%28%28n%21%29%5E2%2A%28n-r%29%21%2A%28n-r-1%29%21%29%2F%28%28n-r%29%21%2A%28n-r-1%29%21%29=0.....(1a)
(1a) can be satisfied if and only if the numerator equals zero.
=>
n=0, trivial solution if r=0.
n=r, leads to (-1)! in denominator, rejected
n-r-1=0, means n=r+1
Thus
The above equation can be satisfied when n=r+1, or
P(n,n-1)=P(n,n) for all n>0.

Note: if there is a typo in the original question, please post a new question.