Question 1014457: Professors Roberts and Jones, who lives 676 miles apart, are exchanging houses and jobs for the summer. They start out for their new locations at exactly the same time, and they meet after 6.5 hours of driving. If their average speeds differ by 4 mph, what are their average speeds?
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Professors Roberts and Jones, who lives 676 miles apart, are exchanging houses and jobs for the summer. They start out for their new locations at exactly the same time, and they meet after 6.5 hours of driving. If their average speeds differ by 4 mph, what are their average speeds?
-------------------------------------------------------------------
6.5*x + 6.5*(x+4) = 676.
where x is the lowest speed.
Simplify and solve:
13x + 26 = 676,
13x = 676 - 26 = 650,
x = 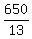 = 50 mph. = 50 mph.
Answer. Slower car speed 50 mph. Faster car speed 54 mph.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Professors Roberts and Jones, who lives 676 miles apart, are exchanging houses and jobs for the summer. They start out for their new locations at exactly the same time, and they meet after 6.5 hours of driving. If their average speeds differ by 4 mph, what are their average speeds?
With slower speed being S, we get: 6.5S + 6.5(S + 4) = 676
Solve to get: Slower and faster speeds: 
|
|
|