.
The coefficient of 5th 6th and 7th terms in the expansion ( 1+a)^7 in ascending powers of a forms the arithmetic progressions. Find the A.P
--------------------------------------------------------------
On binomial expansion see the lesson Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion in this site.
7-th term is 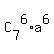 .
6-th term is
.
6-th term is  .
5-th term is
.
5-th term is 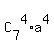 .
.
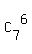 = 7;
= 7;  =
= 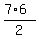 = 21;
= 21;  =
= 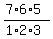 = 35.
This AP is 35, 21, 7. Or 7, 21, 35 from the other end.
= 35.
This AP is 35, 21, 7. Or 7, 21, 35 from the other end.