Question 1014153: The diagonals of a rhombus are in the ratio 1:3. If each side of the rhombus is 10 cm long, find the length of the longer diagonal.
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The diagonals of a rhombus are in the ratio 1:3. If each side of the rhombus is 10 cm long, find the length of the longer diagonal.
----------------------------------------------------------------
Let x be the shorter diagonal measure, in centimeters.
Then the longer diagonal is 3x long, according to the condition.
Diagonals of a rhombus bisect each other at the intersection point (it is true for any parallelogram).
Besides of it, diagonals of a rhombus are perpendicular.
So, they divide the rhombus in four congruent right-angled triangles.
Let us consider one of these four triangles.
It has the legs of  and and 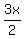 cm.
It has the hypotenuse of 10 units long (it is the side of the rhombus).
Thus you can write the Pythagorean Theorem in this form: cm.
It has the hypotenuse of 10 units long (it is the side of the rhombus).
Thus you can write the Pythagorean Theorem in this form:
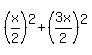 = = 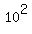 , or , or
 = =  , or , or
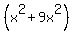 = = 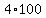 , or , or
 = =  .
Hence, .
Hence,  = = 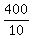 = 40, and x = = 40, and x = 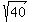 = =  .
It is the length of the shorter diagonal.
The length of the longer diagonal is in 3 times more, or .
It is the length of the shorter diagonal.
The length of the longer diagonal is in 3 times more, or  cm.
Answer. The length of the longer diagonal is cm.
Answer. The length of the longer diagonal is  cm. cm.
|
|
|