Question 1013975: So how would I go about solving this quadratic equation:
y=-1x^2 - 10x
I know the axis of symmetry is -5 because x=-b/2a. When I try to find the y axis however, I get y=25. Is that right? if not, how would I solve this question? Thanks for helping me!
Found 3 solutions by josgarithmetic, macston, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! That is ONE equation with TWO variables, so if that is all, then nothing to "solve". Your "try to find the y axis" makes no sense. The y-axis is the y-axis; the  is not clear.
Best you could do is to look for x and y intercepts, and with whatever skills you know up to now, find axis of symmetry, and the vertex.
Here is what you can do.
meaning the x-axis intercepts are 0 and -10; which you can also call the "roots" of  .
The form of the equation  tells you that you have a vertical axis of symmetry; and it will occur in the exact middle between the x-axis intercepts, as YOU ALREADY FOUND,  to be this symmetry axis.
The vertex happens where , so you find the y-coordinate using 
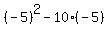
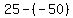
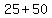
The vertex is (-5,75), and this is a MINIMUM, based on, again, the form of the equation you have.
Answer by macston(5194)  (Show Source):
You can put this solution on YOUR website! It depends on what you want to know.
.
y=-x^2-10x
y=(-1x)(x+10)
.
To find the roots, let y=0
(-1x)(x+10)=0
-1x=0 --OR-- x+10=0
x=0 --OR-- x=-10
Intercepts x axis at 0 and -10.
.
To find the x value at maximum(or minimum):
Set first derivative=0
.
f(x)=-x^2-10x . (original equation)
.
f'(x)=-2x-10 . (first derivative)
0=-2x-10
10=-2x
-5=x
.
The sign of the second derivative tells if
it has a maximum or minimum (if negative,
it has maximum, if positive it has minimum)
f''(x)=-2 . (second derivative)
is negative, so there is a maximum where x=-5.
.
Find y where x=-5:
.
f(x)=-x^2-10x
f(-5)=-(-5)^2-10(-5)=-25=50=25
The maximum is at the point (-5,25),
crosses x-axis at -10 and 0
.
GRAPH:
.
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website! So how would I go about solving this quadratic equation:
y=-1x^2 - 10x
I know the axis of symmetry is -5 because x=-b/2a. When I try to find the y axis however, I get y=25. Is that right? if not, how would I solve this question? Thanks for helping me!
No, that's incorrect! You just found the coordinates of the VERTEX, but you need the solutions/zeroes/roots, instead.
To find the solutions/zeroes/roots, you simply set the equation equal to 0, as follows:  , and solve for x.
You should get: 
|
|
|
