Question 1013927: at a fast food restaurant, a family bought 4 hamburgers and 3 bags of french fries for 4.20. at the same time, a family traveling with them bought 5 hamburgers and 2 bags of french fries for 4.55. what was the cost of one hamburger and one bag of french fries? what was the cost if you ordered 5 hamburgers and 4 french fries?'
Found 2 solutions by ikleyn, lwsshak3:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
At a fast food restaurant, a family bought 4 hamburgers and 3 bags of french fries for 4.20.
At the same time, a family traveling with them bought 5 hamburgers and 2 bags of french fries for 4.55.
What was the cost of one hamburger and one bag of french fries? What was the cost if you ordered 5 hamburgers and 4 french fries?'
------------------------------------------------------------
From the condition, you have this system of two equations in two unknowns
4h + 3f = 420, (1)
5h + 2f = 455. (2)
Here h is the price of one hamburger and f is the price of one bag of french fries in cents.
To solve it, multiply equation (1) by 2 (both sides) and equation (2) by 3. You will get
8g + 6f = 840, (1')
15h + 6f = 1365. (2')
Now distract the equation (1') from (2') (both sides). In this way you eliminate the unknown f and obtain a single equation for unknown h:
15h - 8h = 1365 - 840, or
7h = 525.
Hence, h = 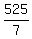 = 75.
Substitute the found value of h = 75 into equation (1). You get
3f = 420 - 4h = 420 -4*75 = 420 - 300 = 120,
f =  = 40.
Thus the cost of one hamburger is $0.75; the cost of one bag of french fries is $0.40.
Now calculate the cost of 5 hamburgers and 4 french fries. It is
5*$0.75 + 4*$0.40 = $5.35.
Answer by lwsshak3(11628)  (Show Source):
You can put this solution on YOUR website! at a fast food restaurant, a family bought 4 hamburgers and 3 bags of french fries for 4.20. at the same time, a family traveling with them bought 5 hamburgers and 2 bags of french fries for 4.55. what was the cost of one hamburger and one bag of french fries? what was the cost if you ordered 5 hamburgers and 4 french fries?'
let h=cost of one hamburger
let f=cost of one bagof french fries
4h+3f=4.20
5h+2f=4.55
8h+6f=8.40 (mult.1st eq by 2)
15h+6f=13.65 (mult.2nd eq by 3)
subtract
7h=5.25
h=.75
3f=4.20-4h=4.20-3.00=1.20
f=.40
cost of one hamburger=75ç
cost of one bag of french fries=40ç
5 hamburgers and 4 bags of french fries cost 5*.75+4*.40= $5.35
|
|
|
