SOLUTION: 2x-y+4z+t=-2 3x+2y-t=-3 x+2y+2t=10 x+y+2z=-2

This comes out with very terrible answers, so I'll bet anything
you copied something wrong, like a number or a sign.  So you'll
probably have to do it over after correcting your error of 
copying, because the tiniest error in a problem like this will
make the answers come out terrible.  But here it is exactly
as you copied it.

Line up the terms with like letters under like letters,
like this: 



Put in all the understood zero terms for missing letters
and understood 1 coefficients:




Move the - signs close to the terms, erase the + signs
and all the letters and put a vertical line where the
= signs are.  Then enclose the whole thing in parentheses.
This is called an augmented matrix, augmented because of
the vertical line:



It's easier if you have a 1 as the upper left element.
So we switch the 1st and 3rd rows.  We write that operation as
R1<->R3



To get a 0 where the 3 is in the 2nd row, 1st column, multiply
R1 by -3 and add R2 to it:

            -3  -6   0  -6  |  30
             3   2   0  -1  |  -3
           ------------------------
             0  -4   0  -7  | -33

Now replace R2 by that.  This operation is written as

-3R1+R2->R2



--
To get a 0 where the 2 is in the 3rd row, 1st column, multiply
R1 by -2 and add R3 to it:

            -2  -4   0  -4  | -20
             2  -1   4   1  |  -2
           ------------------------
             0  -5   4  -3  | -22

Now replace R3 by that.  This operation is written as

-2R1+R2->R2



--
To get a 0 where the 1 is in the 4th row, 1st column, multiply
R1 by -1 and add R4 to it:

            -1  -2   0  -2  | -10
             1   1   2   0  |  -2
           ------------------------
             0  -1   2  -2  | -12

Now replace R4 by that.  This operation is written as

-1R1+R4->R4



Now we work on the second column.  Things will be easier
if we can get a 1 where the -4 is on the 2nd row 2nd column.
So we multiply R3 by -1 and swap it with R2.

That operation is written as

-R4<->R2

 
-----------------------------------------

To get a 0 where the -5 is in the 3rd row, 2nd column, multiply
R2 by 5 and add R3 to it:

             0   5  -10  10  |  60
             0  -5    4  -3  | -22
           ------------------------
             0   0   -6   7  |  38

Now replace R3 by that.  This operation is written as

-5R2+R3->R3


--
To get a 0 where the -4 is in the 4th row, 2nd column, multiply
R2 by 4 and add R4 to it:

             0   4  -8   8  |  48
             0  -4   0  -7  | -33
           ------------------------
             0   0  -8   1  |  15

Now replace R4 by that.  This operation is written as

-4R2+R4->R4



To get a 0 where the -8 is in the 4th row, 3rd column, multiply
R3 by 4, and add -3 times R4 to it:


             0   0  -24  28  | 152
             0   0   24  -3  | -45
           ------------------------
             0   0    0  25  | 107

Now replace R4 by that.  This operation is written as

-4R2-3R4->R4



Convert the augmented matrix back to a system of equations:



Get rid of the understood 0 terms and 1 coefficients:



Solve the 4th equation to find t




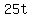
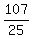Substitute in the 3rd equation to find z




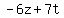
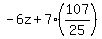
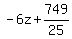Clear of fractions by multiplying through by 25



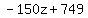
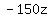
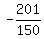Reduce the fraction:


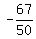Substitute in the 2nd equation to find y




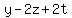
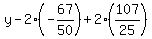
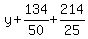Clear of fractions by multiplying through by 50




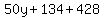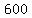
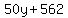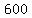
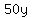
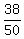Reduce the fraction:


Substitute in the 1st equation to find x




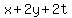
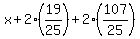
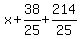Clear of fractions by multiplying through by 25





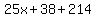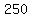
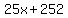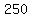
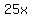
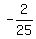So the terrible solution is



Now find your mistake in copying the problem and
re-do it with the correction.

Edwin