SOLUTION: Jason has 46 total coins with a mixture of dimes and quarters. The total value of his coins is $6.55. How many dimes and how many quarters does Jason have?

Click here to see ALL problems on Expressions-with-variables

Question 1013548: Jason has 46 total coins with a mixture of dimes and quarters. The total value of his coins is $6.55. How many dimes and how many quarters does Jason have?
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52794) (Show Source):
You can put this solution on YOUR website!
.
Jason has 46 total coins with a mixture of dimes and quarters. The total value of his coins is $6.55.
How many dimes and how many quarters does Jason have?
---------------------------------------------------------------------------

Let d = # of dimes and q = # of quarters Jason has. Then you have this system of two equations in two unknowns d and q: d + q = 46, (1) 10d + 25q = 655. (2) From (1), express d = 46 - q and substitute it into (2). In this way, you get a single equation for q: 10*(46 - q) + 25q = 655, 460 - 10q + 25q = 655, 15q = 655 -460, 15q = 195, q = 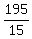= 13. Answer. Jason has 13 quarters and 46 - 13 = 33 dimes.

Answer by Alan3354(69443) (Show Source):
You can put this solution on YOUR website!
Jason has 46 total coins with a mixture of dimes and quarters. The total value of his coins is $6.55. How many dimes and how many quarters does Jason have?
----------
Here's another method.
---
46 dimes = $4.60
Each dime replaced by a quarter adds 15 cents.
655 - 460 = 195
195/15 = 13 replacements.
--> 13 quarters & 33 dimes