Question 1013535: Show that the sum of nth term of the series log3+log6+log12+.... Is nlog3+n(n-1)log2/2
Found 2 solutions by richard1234, Edwin McCravy:
Answer by richard1234(7193)   (Show Source):
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
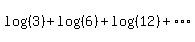We first get the nth term of the sequence
3,6,12,...
That's a geometric series with a1 = 3, r = 2
The nth term of that sequence is a∙rn-1 or 3∙2n-1
So the log series is
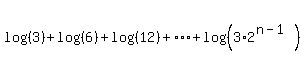We write each number in parentheses as a product of 3 and some
other number:
Now we use the principle that the log of a product equals the sum
of the logs of the factors:
Since there are n terms, there and n log(3)'s added so the above
sequence is:
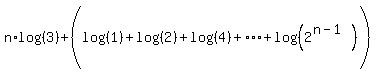We write each number, 1,2,4,...2n-1 in the parentheses are powers of 2.
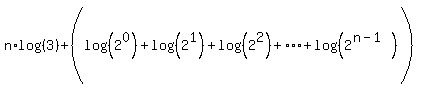Use the principle of logs that says that the log of an exponential is the
exponent times the log of the base:
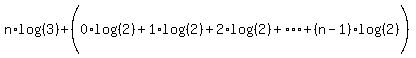We factor out log(2)
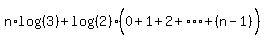The series in parentheses is an arithmetic series with a1 = 0,
common difference 1 and number of terms n. We use the sum formula for
the series in parentheses:
  
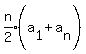
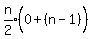
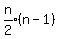Substituting for the series in parentheses:
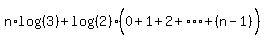
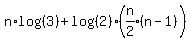
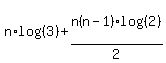Edwin
|
|
|
