SOLUTION: This confuses me, please help me out:what is the remainder when 2014^2015 is divided by 9?

Answer. 4.


Solution


1.

2014 is not divisible by 3.  (The divisibility by 3 rule is divisibility by 3 the sum of the digits of a number. 
                              The sum 2+ 0 + 1 + 4 = 7 in not divisible by 3.
                              See the lesson Divisibility by 3 rule in this site).

Hence,   is not divisible by 9.


2.

The remainder of division 2014 by 9 is 7   (You can check it yourself by making long division. 
                                            By the way, it coincides with the number 7 above, and it is not occasional). 

The remainder of division  by 9 is the same as the remainder of division  = 49 by 9 and is 4.  
                                           (I refer to elementary number theory, but you can check it yourself).

The remainder of division  by 9 is the same as the remainder of division  = 343 by 9 and is 1.  
                                           (Again, I refer to elementary number theory, but you can check it yourself).

After that the remainders of division 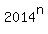 by 9 will repeat again and again in the loop 7, 4, 1, 7, 4, 1, . . . 
                                           periodically/cyclically with the cycle length 3.

So, the sequence of remainders of divisions 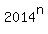 by 9 is 

7, 4, 1, 7, 4, 1, . . . for n = 1, 2, 3, 4, 5, 6 . . . , (1)

i.e. is cyclical with the cycle length 3.

Thus when you get , the remainder will be WHAT?

Divide 2015 by 3 and you will get the remainder 2.

So, the number of interest is the second number in the sequence of remainders (1), i.e. 4.