SOLUTION: If 1/(a-(-w))-(-1)/(b-(-w))-(-1)/(c -(-w))-(-1)/(d-(-w))=2w^2 and 1/(a-(-w^2))-(-1)/(b-(-w^2))-(-1)/(c-(-w^2))-(-1)/(d-(-w^2))=2w then prove that 1/(a-(-1))-(-1)/(b-(-1))-(-1)/(c-

Now your formulas look much better.

Thank you for following my instructions.

Now tell us please what is  in these formulas.

OK, very good. 

So,  w = 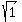 =  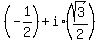 is this complex number.

Let me rewrite what is given and what you want to prove in an equivalent, but simpler form:

If 

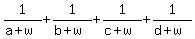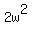 =           (1)    and 

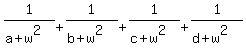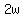 =     (2)    then prove that 

 = .

Let us add the formulas (1) and (2) term-by-term. I will start with the pair of addends with the symbol "a", and will simplify it step by step:

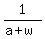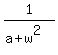 +  =             (write with the common denominator and then add the numerators. You will get)

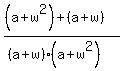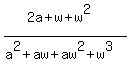=  =  =   (now recall that  = 1. So, replace  by 1 in the last formula. You will get)

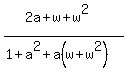=  =   (now use the fact that for your special number "w" there is the identity  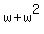 = -1. 
                          So, substitute it into the last formula. You will get)
= .

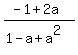OK. It looks like I can not simplify it further.

You can make this trick with every other pair of addends containing the symbols "b", "c" and "d". 
In this way you will obtain similar formulas.

Now, when you add right sides of these long formulas, you will get 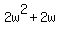.  It  equals  -2  based on what was noted above.

Finally, after adding these long formulas and simplifications, you get

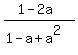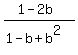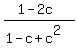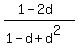 +  +  +  = 2.

It is not exactly what you requested.
But it is what our mother-nature allows us to do.