Question 1012778: Verify that the triangle wiith vertices P(-3,2) Q(2,5) and R(2,-1) is an isosceles triangle. find the midpoint M, of the side PR and the midpoint, N, of the side PQ
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Verify that the triangle with vertices P(-3,2) Q(2,5) and R(2,-1) is an isosceles triangle. find the midpoint M, of the side PR and the midpoint, N, of the side PQ
--------------------------------------------------------------------
The segment PQ has coordinates (5,3).
The square of its length is 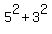 = 25 + 9 = 34. = 25 + 9 = 34.
The segment PR has coordinates (5,-3).
The square of its length is  = 34. = 34.
Since |PQ| = |PR|, the triangle PQR is isosceles.
midpoint M = (-0.5,0.5).
midpoint N = (-0.5,3.5).
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Verify that the triangle wiith vertices P(-3,2) Q(2,5) and R(2,-1) is an isosceles triangle. find the midpoint M, of the side PR and the midpoint, N, of the side PQ
Since Q (2, 5) and R (2, - 1) have the same x=coordinate:2, it follows that QR is a horizontal line that is parallel to the x-axis. Thus, QR's distance
is merely the difference between the points' y-coordinates. This means that the distance of QR is: = 5 - - 1, or 5 + 1, or 6 units.
This makes it easier to determine what type of triangle this is, as now, you just need to find the distances of PQ and PR.
If 2 sides are found to be congruent, then it being an isosceles triangle would be proven.
|
|
|