Question 1012777: Show algebraically that this triangle is a right triangle. The triangle has the vertices P(-4,-3) Q(2,5) R(4,1)
Find the midpoint of the hypotenuse.
Show that this midpoint is equidistant from each of the vertices
Thanks!
Found 3 solutions by Alan3354, KMST, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Show algebraically that this triangle is a right triangle. The triangle has the vertices P(-4,-3) Q(2,5) R(4,1)
-------------
Find the lengths of the 3 sides. Label the longest c.
If  it's a right triangle. o/w it's not. it's a right triangle. o/w it's not.
===================
Find the midpoint of the hypotenuse.
Show that this midpoint is equidistant from each of the vertices
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two ways to show that the triangle is a right triangle.
You could find that two of the sides are perpendicular, or
you could find that the square of the length of one side is the sum of the squares of the lengths of the other two sides.
USING THE LENGTHS OF THE SIDES:




So, by the converse of the Pythagorean theorem,
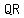 and and  are the legs of a right triangle with hypotenuse are the legs of a right triangle with hypotenuse  . .
PROVING THAT TWO SIDES ARE PERPENDICULAR:
IF you have learned about slope of a line,
you may also have learned that if two lines have slopes whose product is  , those lines are perpendicular. , those lines are perpendicular.
Slope of  = =
Slope of 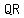 = =
The product of the slopes is  , ,
so  and and 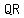 are perpendicular, are perpendicular,
which means that triangle 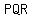 is a right triangle, is a right triangle,
with a right angle at  and hypotenuse and hypotenuse  . .
MIDPOINT OF THE HYPOTENUSE:
The coordinates of 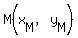 , the midpoint of hypotenuse , the midpoint of hypotenuse  , are found by averaging the coordinates of , are found by averaging the coordinates of  and and  : :


DISTANCES FROM 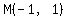 TO TO  , ,  , and , and  : :
To show that the distances are the same, we can just show that their squares are the same.


 . .
So, the distances from  to to  , ,  , and , and  are all are all  . .
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show algebraically that this triangle is a right triangle. The triangle has the vertices P(-4,-3) Q(2,5) R(4,1)
Find the midpoint of the hypotenuse.
Show that this midpoint is equidistant from each of the vertices
---------------------------------------------------------------
By the way, in an right-angled triangle, the midpoint of the hypotenuse is equidistant from each of the vertices.
See the lesson Median drawn to the hypotenuse of a right triangle in this site.
It is true for any right-angled triangle.
|
|
|