SOLUTION: How to solve this problem Johnson family bought 4 adult tickets and 2 child tickets for a total of $37 to the movies. And the Gonzalez family bought 3 adult tickets and 4 c

From the condition, you have this system of two equations:

4a + 2c = 37,   (1)
3a + 4c = 39.   (2)

where unknowns a and c are the ticket costs for adult and children respectively.

To solve it, multiply equation (1) by (-2) (both sides) and then add to the equation (2). You will get

-8a + 3a = -2*37 + 39,   or

-5a = -35.

Therefore, a = 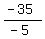 = 7 dollars is the price for the adult ticket.

Now try yourself to complete the solution.