|
Question 1012281: i would like to receive help with this question. " A cylindrical shaped cup has a height of 7 centimeters and a volume of 112 pi cubic centimeters. Henry fills the cup completely full of water. He then pours the water from the cup into a cone. If the cone has a radius twice the measure of the cup, What is the height of the cone? "
Found 2 solutions by Theo, KMST:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! cylinder height = 7 cm and volume - 112 * pi cubic cm.
henry fills the cup with water all the way to the top.
he then pours all the water into a cone.
presumably this also fills up the cone.
the cone has double the radius of the cylinder.
what is the height?
the volume of the cone must be the same as the volume of the cylinder.
the formula for the volume of a cone is v = 1/3 * pi * r^2 * h
the radius of the cone is twice the radius of the cylinder.
the radius of the cylinder is is not provided so we have to solve for it.
the formula for the volume of a cylinder is pi * r^2 * h.
since the volume is 112, the formula becomes 112 = pi * r^2 * 7, because the height is given as 7 cm.
we can solve for r^2 to get r^2 = 112 / (pi * 7) which becomes r^2 = 16 / pi.
solve for r to get r = 4 * sqrt(pi).
since the radius of the cone is twice the radius of the cylinder, then the radius of the cone is 8 * sqrt(pi).
we get formula for the volume of the cone becomes 112 = 1/3 * pi * (8 * sqrt(pi))^2 * h
solve for h to get h = 112 / (1/3 * (8 * sqrt(pi))^2)
simplify to get h = (112 * 3) / (64 * pi) which becomes h = 336 / (64 * pi) which becomes h = 5.25 cm.
so, we have:
r for the cylinder = 4/sqrt(pi)
h for the cylinder = 7
r for the cone = 8/sqrt(pi)
h for the cylinder = 5.25
volume for each = 112.
formula for volume of a cylinder is v = pi * r^2 * h.
v = 112
r = 4/sqrt(pi), r^2 = 16/pi
h = 7
formula becomes 112 = pi * 16/pi * 7 = 16 * 7 = 112.
this checks out ok.
formula for volume of a cone is v = 1/3 * pi * r^2 * h.
v = 112
r = 8/sqrt(pi), r^2 = 64/pi
h = 5.25
formula becomes 112 = 1/3 * pi * 64/pi * 5.25 = 1/3 * 64 * 5.25 = 112.
this checks out ok as well.
your solution is that the height of the cone is 5.25 centimeters.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! We have to solve for the radius of the cylinder
IF we are not expected to be good enough at algebra.
That must be the case, since we are given the volume as encouragement to work hard ans solve for the radius og the cylinder.
However, the volume and the radius of the cylinder are not needed to solve the problem.
For a cylinder of radius  and height  ,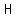
 .
For Henry's cylinder, of radius  and height  (both in cm),
 , in cubic centimeters.
For a cone of radius and height ,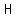
 .
For Henry's cone, of radius  , height  (both in cm), and , in cubic centimeters,
 -->  .
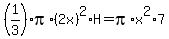
So, assuming the cup of water filled the cone completely, without any spillover,
the height of Henry's cone is  .
|
|
|
| |
