Question 1012214: The effects on the graph of the linear parent function,f(x)=x,are described below.
•Reflection over the x axis
•Vertical compression by a scale factor of 0.5
•Horizontal shift of 4 units to the right
•Vertical shift of 3 units down
What function could be used to represent the transformed linear parent function?
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
 ,are described below.
•Reflection over the  axis:
-f (x) reflects f (x) over the x-axis
 ->Our new line has negative slope.
•Vertical compression by a scale factor of  :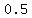
f (ax) stretches/compresses f (x) horizontally
if 0 < a < 1 (a fraction), the graph is stretched horizontally by a factor
of a units.
if a > 1, the graph is compressed horizontally by a factor of a units.
if a should be negative, the horizontal compression or horizontal stretching of the graph is followed by a reflection of the graph across the y-axis.
a f (x) stretches/compresses f (x) vertically
if 0 < a < 1 (a fraction), the graph is compressed vertically by a factor
of a units.
if a > 1, the graph is stretched vertically by a factor of a units.
If a should be negative, then the vertical compression or vertical stretching of the graph is followed by a reflection across the x-axis.
•Horizontal shift of  units to the right:
f (x + a) translates f (x) horizontally
if a > 0, the graph translates (slides) to the right.
if a < 0, the graph translates (slides) to the left.
•Vertical shift of  units down:
f (x)+ a translates f (x) vertically
if a > 0, the graph translates (slides) upward.
if a < 0, the graph translates (slides)
downward.
|
|
|
