Question 1012078: For each exponential function, state the domain and range, whether the function increases or decreases, and the y-intercept.
a) y=2(4)^x
b) y=3(1/2)^x
c) y=-(0.3)^x
d) y=-3(5.2)^x
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! in all of these, the domain is all real values of x
the range and the y-intercept for each is shown below:
a) y=2(4)^x
the range is all real value of y > 0.
the y-intercept is y = 2 * 4^0 = 2*1 = 2.
the function is increasing form left to right.
that's the red equation in the graph shown below.
b) y=3(1/2)^x
the range is all real values of y > 0.
the y-intercept is y = 3 * (1/2)^0 = 3 * 1 = 3.
the function is decreasing from left to right.
that's the blue equation in the graph shown below.
c) y=-(0.3)^x
the range is all real values of y < 0.
the y-intercept is equal to -(0.3)^0 = -1.
the graph is increasing from left to right.
that's the green equation in the graph shown below.
d) y=-3(5.2)^x
the range is all real values of y < 0.
the y-intercept is equal to -3 * (5.2)^0 = -3 * 1 = -3.
the graph is decreasing from left to right.
that's the purple equation in the graph shown below:
see below the graph for further comments.
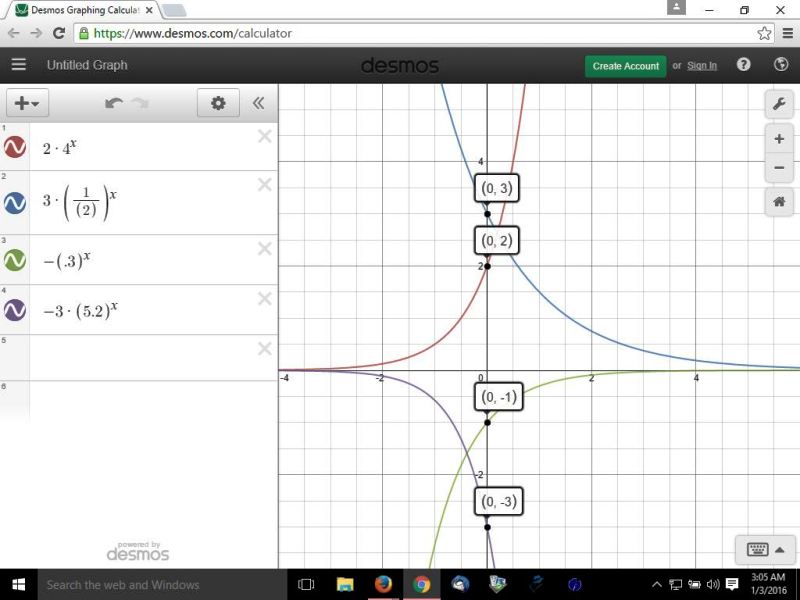
2*4^x is increasing because, as x gets larger, 4^x gets larger.
3*(1/2)^x is decreasing because, as x gets larger, (1/2)^x gets smaller.
(1/2)^1 = 1/2
(1/2)^2 = 1/4
etc.
-.3^x is increasing because, as x gets larger, .3^x gets smaller and so minus .3^x gets larger.
.3^1 = .3
.3^2 = .09
.09 is smaller than .3
-.3^1 = -.3
-.3^2 = -.09
-.09 is larger than -.3
-3*5.2^x is decreasing because, as x gets larger, 5.2^x gets larger and so minus 5.2^x gets smaller.
5.2^1 = 5.2
5.2^2 = 27.04
27.04 is larger than 5.2
-5.2^1 = -5.2
-5.2^2 = -27.04
-27.04 is smaller than -5.2
|
|
|