Question 1012011: Expand the expression using the binomial theorem.
(x-1/x)^3
Got stuck on this question for hours. Thank you.
Found 2 solutions by ValorousDawn, MathTherapy:
Answer by ValorousDawn(53)   (Show Source):
You can put this solution on YOUR website! I won't give you the full treatment of the binomial theorem, because the explanation is unwieldy. Do you know about Pascal's triangle?
Since the expression is raised to the third degree, you use the fourth row of Pascal's triangle. The numbers are 1, 3, 3, 1, which are the coefficients of our sum.
Then you raise the first term (x) to the degree (3), and each subsequent term, you divide away an x, and multiply your other term (1/x) until you get your second term (1/x) to the degree (3), with each term going with the corresponding number in pascals triangle as a coefficient.
So. 
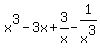
Answer by MathTherapy(10552)  (Show Source):
|
|
|
