Question 1011732: cot(x)*cot(2 x) = 1
Found 2 solutions by Edwin McCravy, Alan3354:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!   
We normally aren't given double angle formulas for cotangents.
We usually only are given double angle formulas for tangents.
Since we know that  , let's
convert to tangents:
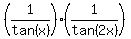
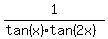We take reciprocals of both sides, and since the reciprocal
of 1 is 1, we have
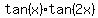We use the double-angle formula that we are always given:
which is 
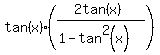
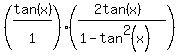
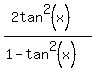Multiply both sides by the denominator on the left:
 
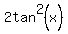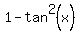Solve for tan2(x)
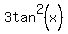
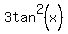Take square roots
 
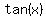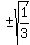
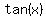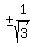Remembering the special 30°-60°-90° right triangle:
we know by the ± that the angle can be in any quadrant
with a 30° reference angle, so the solutions are
30°, 150°, 210°, 330° plus any integer n times 360°.
or in radians
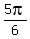 , , , plus any integer n times  .
Edwin
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! cot(x)*cot(2 x) = 1
---
If you want to solve for x:
cot(2x) = (cot^2(x) - 1)/(2cot(x))
--> cot(x)*(cot^2(x) - 1)/(2cot(x)) = 1
(cot^2(x) - 1)/2 = 1
cot^2(x) = 3
tan^2(x) = 1/3
x = pi/6 + n*pi, n = ± 0,1,2,3...
|
|
|
