Question 1011618: A jet can fly 550mph in calm air .Traveling with the wind, the plane can fly 2520 miles in the same amount of time as it flies 1880 miles against the wind .... Find the time and rate of wind ? Please show how you solved it
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! The same question is often asked for help but in different examples. The solution to be started here will be generalized and suitable for all examples of this type of problem.
Definition of Variables
r, speed when no wind, calm air
w, speed of wind
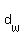 , distance done with the wind , distance done with the wind
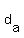 , distance done against the wind , distance done against the wind
t, time at which the two distances were found
speed time distance
WITH r+w t 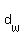 AGAINST r-w t
AGAINST r-w t 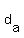
Variables given values: 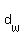 , , 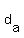 , r , r
Unknown variables: w, t
Using RT=D the basic travel rates rule, the description and data table formed with it gives enough to solve for w and t.

The reason that the first equation was formed and included is because it uses only ONE unknown variable, w, which can then be used in either of the next two equations to solve for t.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A jet can fly 550mph in calm air .Traveling with the wind, the plane can fly 2520 miles in the same amount of time as it flies 1880 miles against the wind .... Find the time and rate of wind ? Please show how you solved it
Let speed of wind be, W
Then 
1,880(550 + W) = 2,520(550 - W) --------- Cross-multiplying
1,880(550) + 1,880W = 2,520(550) - 2,520W
1,880W + 2,520W = 2,520(550) - 1,880(550)
4,400W = 640(550)
80(55W) = 80(8)(550)
 (55W) = (55W) =  (8)(550) (8)(550)
55W = 8(550)
W, or speed of wind = 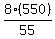 , or , or  mph mph
Time taken to cover each distance: 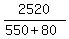 , or , or 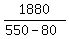 --------> -------->  hours hours
|
|
|