Question 1011610: A 6-digit number begins with a 1. However, if the 1 is put at the end of the number instead of at the start,
the resulting 6-digit number is 3 times the original number. Find the number.
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
A 6-digit number begins with a 1. However, if the 1 is put at the end of the number instead of at the start,
the resulting 6-digit number is 3 times the original number. Find the number.
-------------------------------------------------------------------
We can write the given 6-digit number starting with 1 as
n = 100000 + a,
where 100000 is the number produced by the "1" in the most left position,
and "a" is the number written by the digits in positions from 2 to 6.
When the "1" is put at the end, we get the number
m = 10a + 1.
Now, the condition says that 3n = m. It gives you an equation for a:
3*(100000 + a) = 10a + 1.
Simplify and solve it:
30000 + 3a = 10a +1,
7a = 299999,
a = 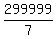 = 42857.
So, the original number was 142857.
|
|
|
