SOLUTION: The vertices of a triangle are (1,k), (4,-3) and (-9,7). If the area of triangle is 15 Sq. units, then find the value(s) of k.

Algebra ->  Length-and-distance -> SOLUTION: The vertices of a triangle are (1,k), (4,-3) and (-9,7). If the area of triangle is 15 Sq. units, then find the value(s) of k.       Log On


   

Question 1011415: The vertices of a triangle are (1,k), (4,-3) and (-9,7). If the area of triangle is 15 Sq. units, then find the value(s) of k.
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
The vertices of a triangle are:
(1,k),
(4,-3) and
(-9,7).
If the area of triangle is A=15+ Sq. units, then find the value(s) of k.

We have a formula which can be directly used on the vertices of triangle to find its area.
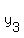If, (x%5B1%5D, y%5B1%5D), (x%5B2%5D, y%5B2%5D) and (x%5B3%5D, y%5B3%5D) are the
coordinates of vertices of triangle then area of triangle is:


you are given:
A=15+ Sq. units
x%5B1%5D=1
x%5B2%5D=4
x%5B3%5D=-9
y%5B1%5D=k
y%5B2%5D=-3
y%5B3%5D=7
substitute it in

15=+%281%2F2%29%281%2A%28-3-7%29%2B4%287-k%29%2B%28-9%29%28k%2B3%29%29
30=+%28-10%2B28-4k-9k-27%29
30=+-10%2B28-4k-9k-27
30=+-37%2B28-13k
30=+-9-13k
13k=+-9-30
13k=+-39
k=+-39%2F13
k=+-3
so, your points are:
(1,-3),
(4,-3) and
(-9,7)


ss you can see from the graph, the length of the base of triangle is 3 units and height is 10 units
so, the area is: A=%281%2F2%29b%2Ah=>A=%281%2F2%293%2A10=>A=30%2F2=>A=15 sq.units and it confirms that k=-3